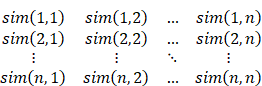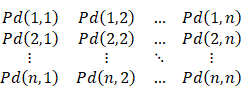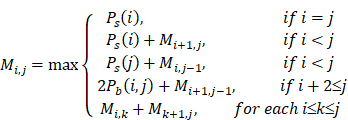10
Impact Factor
ISSN: 1449-2288
Int J Biol Sci 2018; 14(8):872-882. doi:10.7150/ijbs.24595 This issue Cite
Research Paper
Research on folding diversity in statistical learning methods for RNA secondary structure prediction
1. College of Computer Science, Sichuan University, China
2. College of Chemistry, Sichuan University, China
3. Vice Dean of College of Computer Science, Sichuan University
4. Department of Computer Science and Information Technology, La Trobe University, Australia
*These authors contributed equally to this work and should be considered co-first authors
Received 2017-12-27; Accepted 2018-2-21; Published 2018-5-22
Abstract
How to improve the prediction accuracy of RNA secondary structure is currently a hot topic. The existing prediction methods for a single sequence do not fully consider the folding diversity which may occur among RNAs with different functions or sources. This paper explores the relationship between folding diversity and prediction accuracy, and puts forward a new method to improve the prediction accuracy of RNA secondary structure. Our research investigates the following: 1. The folding feature based on stochastic context-free grammar is proposed. By using dimension reduction and clustering techniques, some public data sets are analyzed. The results show that there is significant folding diversity among different RNA families. 2. To assign folding rules to RNAs without structural information, a classification method based on production probability is proposed. The experimental results show that the classification method proposed in this paper can effectively classify the RNAs of unknown structure. 3. Based on the existing prediction methods of statistical learning models, an RNA secondary structure prediction framework is proposed, namely “Cluster - Training - Parameter Selection - Prediction”. The results show that, with information on folding diversity, prediction accuracy can be significantly improved.
Keywords: RNA secondary structure prediction, statistical learning model, folding diversity, stochastic context-free grammar
Introduction
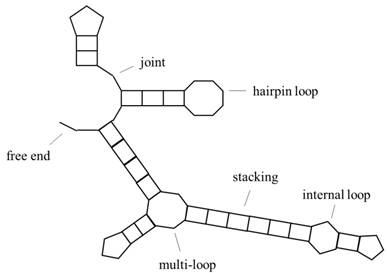
Predicting RNA secondary structure is one of the basic subjects of bioinformatics, and how to improve the prediction accuracy of RNA secondary structure is a hotspot in international research. RNA is divided into two categories, one is mRNA, which can be encoded; the other does not have a coding function but has the ability of gene regulation, called ncRNA, both of which have important biological significance. The specific structural information of RNA is particularly important, because of the principle of the structure-determining-function. RNA primary structure refers to base sequence information, secondary structure refers to base pairing, and tertiary structure refers to the three-dimensional morphology, including base pairing and some other interactions of the base in three-dimensional space. Tertiary structures are often obtained by experimental methods, such as x-ray crystallography or magnetic resonance, but they are expensive and difficult, so we often predict RNA secondary structures. Fig. 1 is a representation of RNA secondary structure, and the object of this paper is a secondary structure without pseudoknots (the study of pseudoknots can be found in the literature[1] [2]). In addition, the conversion of RNA pseudoknots to knot-free structures is studied in the literature[3].
To predict RNA secondary structure, it is common to input the base sequence and return the base pairing relationship to obtain the prediction structure which will be compared with the reference structure to measure prediction accuracy.
Schematic representation of RNA secondary structure. It includes hairpin loop, internal loop, multi-loop, stacking, free end, joint and other structures.
There are two types of RNA secondary prediction methods: the multi-sequence prediction method and the single sequence prediction method. The multi-sequence prediction method is based on multiple homologous RNA sequences to deduce its common secondary structure by using a homologous contrast model, and although it is still the most accurate prediction method, it needs to provide multiple homologous sequences for each RNA to be predicted, so its application scope is limited[4]. Single-sequence prediction methods use a set of parameters to predict the secondary structure of each RNA sequence. At present, the thermodynamic model and statistical learning model are used frequently.
The thermodynamics model determines the structure of low free energy in a reasonable time using a dynamic programming algorithm, and predicts the secondary structure of RNA according to the optimal solution and the set of some suboptimal solutions. Most of the current thermodynamic models are based on the Minimum Free Energy algorithm (MFE)[5] and the Maximum Expected Accuracy algorithm (MEA)[6]. In order to improve the accuracy of prediction, a large number of thermodynamic parameters are needed, however parameterization is laborious, since it requires calorimetry measurements of many model RNA structures, which greatly limits the development of the thermodynamic model[7, 8].
The statistical learning model trains the parameters to describe the folding rules and predicts the unknown RNA structures via the use of the existing known structure of the RNA[9]. As the number of known RNAs increases, the reliable training set becomes larger and larger, and the prediction accuracy can be improved gradually. The existing statistical learning models mainly use the covariant model algorithm[10] and the Pfold algorithm[11] based on stochastic context-free grammar (SCFG). However, too many structural features will make it difficult to continue to enhance the accuracy (computing time will increase sharply, at the same time there are some structure features not commonly appearing in most RNAs, it will cause redundancy problem).
For the existing single-sequence RNA secondary structure prediction methods, neither thermodynamic models nor statistical learning models fully consider the diversity among RNAs with different functions or different sources. For different RNA, cell environments are various, and folding rules are diverse, but as the forecast methods only use a set of parameters for prediction, the parameters need to take into account the diverse folding rules.
In view of this, we hypothesize that the use of different parameters for different RNAs could improve the prediction accuracy of existing methods. This research focuses on the following three aspects:
- Is there any difference in the folding rules of different RNAs?
- How to assign a folding rule to the RNA to be predicted?
- How to use the information on the differences in folding rules to improve the prediction accuracy?
Results
Existence of Folding Diversity
In this paper, we propose the existence of differences in folding rules, and the definition and extraction of folding rules can be seen in the Materials and Methods Section.
The number of folding rule features is different for various folding rule grammar models. Table 1 shows the number of parameters of five typical grammar models[12].
This paper only takes g6, g6s and basic_grammar for analysis in order to avoid feature redundancy. The experimental data is the public data from 22 families of Rfam [details can be seen in Materials and Methods].
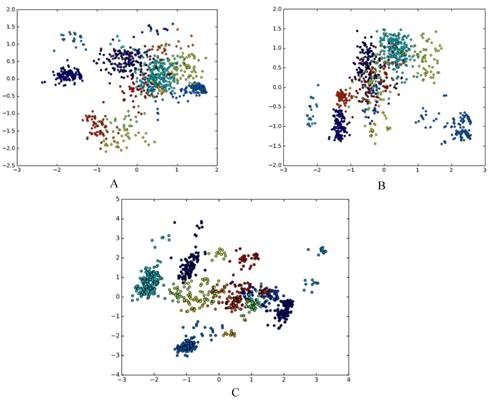
The results are presented using qualitative research via dimensionality reduction analysis in a visualized way and using quantitative research via cluster analysis. We use principal component analysis (PCA) for dimensionality reduction[13]. PCA maps high-dimensional data into a low-dimensional space by linear transformation, and makes the variance of the data in the low-dimensional dimension the largest, in order to preserve the original data information as much as possible. There are other methods for reducing feature dimension, for example, ANOVA[14], binomial distribution[15], and F-score[16]. In this paper, PCA is used to reduce the dimension of the grammatical model, and the dimension-reduced data is plotted on a scatter plot, as shown in Fig. 2A, Fig. 2B and Fig. 2C.
Number of features of grammar models with different folding rules
| grammar model | Number of independent features | |
|---|---|---|
| (6bps) | (16bps) | |
| g6 | 11 | 21 |
| g6s | 261 | 41 |
| basic_grammar | 532 | 572 |
| CONTRAfoldG | 1278 | 5448 |
| ViennaRNAG | 14307 | 90497 |
Each point corresponds to an RNA, the color of each point indicates the family to which it belongs, and different families are distinguished by different colors. It can be seen that there are obvious clusters, and these clusters are closely related to families. This confirms the existence of different folding rules of various RNA families from the qualitative perspective.
A. The g6 feature of DataSetB is reduced to 2D; B. The g6s feature of DataSetB is reduced to 2D; C. The basic_grammar feature of DataSetB is reduced to 2D.
The object analyzed in this paper does not need to consider the spatial form of clustering, so we use an agglomerative hierarchical clustering approach (starting with a single sample and clustering together from the bottom up). ARI (Adjusted Rand Index) is used as the measurement index. The clustering effect of the three grammar models with a different number of clusters is shown in Fig. 3.
Comparison of clustering effect of different grammars and a different class number of clusters
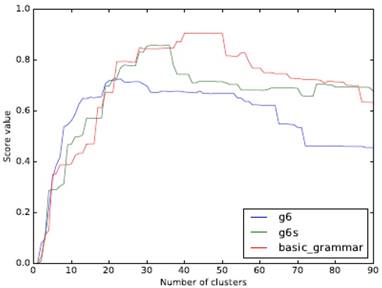
Our experimental data contains 22 families of RNAs. From the figure, it can be seen that a higher API peak value can be obtained if a model with more features is used. When the number of clusters and the number of RNA families are close, the ARI of g6 can be the maximum. The peaks of both g6s and basic_grammar appear after the number of clusters exceeds 22, and the peak value of basic_grammar with more parameters can reach 0.9 or so.
This confirms the diversity of folding rules and the difference of RNA families can be consistent, and when the grammar with many features is used, the number of clusters of the peak value is more than the number of RNA families, which indicates that there is a possibility of further subdivision of the existing family system and may be able to provide reference for the improvement of existing family division.
The two results verify the existence of the diversity of folding rules among various RNA families from the qualitative view and the quantitative perspectives, respectively.
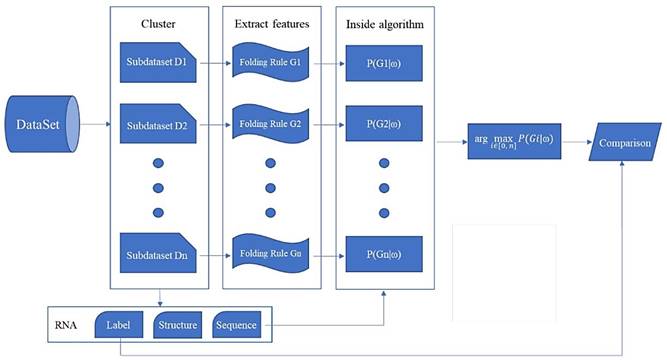
Assign the Folding Rule to the RNA to Be Predicted
We propose a method based on the stochastic context-free grammar (SCFG) generation probability to classify the folding rules of RNA with unknown structures. If we only have sequence information and no structural information, we cannot get the folding rule for RNAs with unknown structures directly. So, we consider clustering for RNAs with known structures, extract a folding rule for each cluster, and obtain the probability of each folding rule generating a certain RNA sequence, then the folding rule with the maximum probability is assigned to the RNA with an unknown structure. According to the above clustering, DataSetD can be divided into n clusters and we can obtain a folding rule Gi for each sub-dataset Di (i∈[0,n]) to reflect the common information of the whole cluster. We assign a class label i to an RNA sequence ω, such that when the RNA sequence is ω, the probability that the folding rule is Gi is the maximum, i.e. for a given RNA sequence ω, find a Gi from the folding rules, such that P(Gi |ω) is the maximum, and return i:
L(ω) = arg maxi∈[0,n] P(Gi | ω)
This paper uses the inside algorithm on each folding rule Gi to obtain the inside variable, and we can get the P (ω| Gi), then the conditional probability P(Gi |ω) of Gi generating the given ω can be derived via the Bayesian formula, finally we can choose the most suitable class i.
The overall flow of the classification experiment proposed in this paper is shown in Fig. 4.
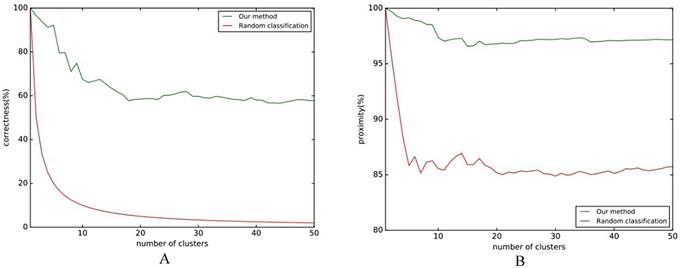
The results of Fig. 5A show that the classification effect is good when the number of clusters is not large, and it will be stable at around 60%. Regardless of how many clusters there are, the classification accuracy rate is higher than the baseline. Fig. 5B shows that the similarity of classification is stable at around 97%. No matter what kind of evaluation index is chosen, the classification effect of this method is higher than the baseline, which shows that this method can effectively classify the differences in folding rules.
Folding rule classification experiment flow chart. A comparison of the effect of the classification with the reference line is shown in Fig. 5, where the reference line in Fig. 5A indicates the correct rate of random classification, and the reference line in Fig. 5B indicates the average similarity.
A. Classification correct rate; B. Classification approximation.
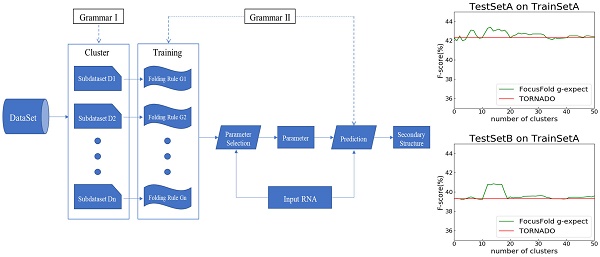
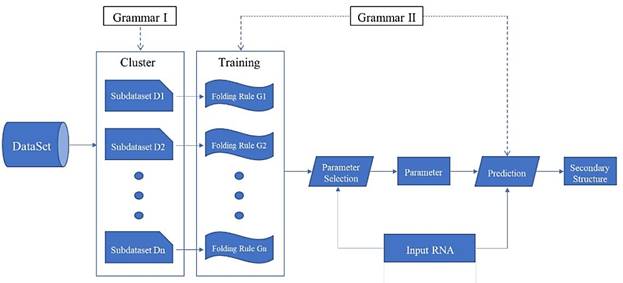
"Clustering - Training - Parameter selection - Prediction" framework diagram
Prediction Framework
We propose a prediction framework for RNA secondary structure. The existing methods based on the statistical learning model enhance the prediction effect mainly by adding features[17], but it is now difficult to find more new features. By considering the differences in folding rules, this paper proposes a prediction framework of RNA secondary structure based on "cluster-training-parameter selection- prediction" (Fig. 6).
The clustering module divides the training data into a plurality of sub-dataset Di according to the differences in the folding rules. The training module extracts a corresponding folding rule Gi for each sub-dataset Di. The parameter selection module selects the parameter that best matches its folding rule according to the different RNA sequence ω that is input. The prediction module predicts the secondary structure of ω using the selected parameters. Each module of the framework can be replaced independently, and can be achieved by using different algorithms. Since the folding rules generated by the training module are used in the prediction module, the grammar of the two modules must be consistent. Clustering and training methods have been mentioned above, so the key is how to choose the parameters and make predictions.
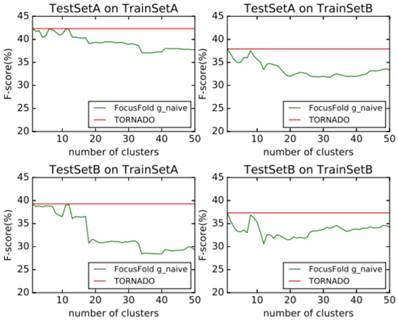
It can be seen that the framework proposed in this paper cannot improve the forecasting result when using the naive classification of the parameters. When using TrainSetA, we set the number of clusters to between 11 to 17, and the accuracy of the proposed method has a significant improvement for the two test sets, about 1% effect improvement for TestSetA and about 1.5% effect improvement for TestSetB compared with TORNADO (a specific parser for a large spectrum of RNA grammars, discussed in the literature[12]); when using TrainSetB, accuracy can obviously be improved about 2.5% effect with the number of clusters between 30 to 50 for TestSetB because of the same source, while there is no effect for TestSetA with different sources. TrainSetA comes from a variety of data, including rich types of folding rules. TrainSetB consists of the 22 families of RNAs obtained from Rfam, and most of them are homologous RNAs. It can be seen that TrainSetA contains more diversity in relation to folding rules, and TrainSetB is relatively simple, so the two will produce different experimental results.
In this paper, the enhancement of the prediction effect is only related to the training data, and is not related to the prediction of data. This indicates that if the diversity rules of the training data are expanded, and the difference in the rules of the training set is analyzed and the most suitable cluster number is found, the forecasting framework proposed in this paper will significantly improve the prediction effect of the existing methods.
Naive classification prediction
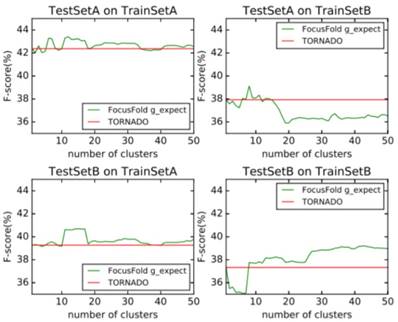
Probabilistic weighted prediction
Comparison
RGRNA[18], proposed recently, combines the heuristic algorithm and the minimum free energy algorithm, allows not only the global search of stems, but also considers the influence of free energy on structure and fits the nested branching structure of RNA molecules. Next, we compared FocusFold (our method) and RGRNA. Training set is TrainSetA, which includes rich types of folding rules, and test set are TestSetA and TestSetB, separately. The number of clusters is between 10~20, and comparison results are shown in Fig. 9.
Comparison of FocusFold and RGRNA. A: TrainSetA as training set, and TestSetA as test set; B: TrainSetA as training set, and TestSetB as test set.
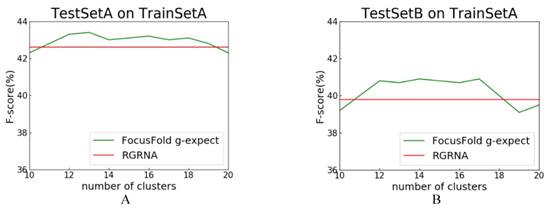
F-score is still the evaluation index. Because RGRNA does not consider clustering, its performance is a horizontal line. For these data sets, when the clustering number is 11~17, and the FocusFold is better. The final result shows that, FocusFold which considered folding diversity is superior to RGRNA.
Discussion
In this paper, we propose the feature of folding rules based on stochastic context-free grammar (SCFG). The diversity of RNA folding rules is confirmed by dimension reduction and cluster analysis, and the relationship between folding rules and family is also confirmed. Furthermore, there is a possibility of further subdivision of the existing family system, and it may be able to provide a reference for the improvement of the existing family division method and the exploration of the RNA function in the same family. In this paper, a classification scheme based on generation probability is proposed to obtain the folding rule of an RNA with an unknown structure. In addition to classification accuracy, a classification approximation is proposed as an evaluation index. At the same time, this paper also proposes the framework of RNA secondary structure prediction of "cluster-training-selection-prediction", and puts forward the probability-weighted method to select the appropriate parameter for the RNA to be predicted. Each module of the framework can be replaced independently, and can be achieved by using different algorithms. Establishing a webserver based on the proposed method will provide convenience to most of wet-experimental scholars[19-22], thus, in the future, we will improve the prediction performance and construct a free online webserver.
Materials and Methods
DataSet
The data used in this paper is the same as that used in the literature[12], which comes from a public dataset[12], including two training sets, TrainSetA and TrainSetB, and two test sets, TestSetA and TestSetB, so that we can compare the prediction accuracy with TORNADO under the same conditions. All of these are open and reliable.
To reduce redundancy, almost identical sequences and similar sequences among the four sets are removed from TrainSetA and nearly identical sequences within the RNA families and similar sequences between families are also removed from TestSetA. The operational definitions we used to generate TrainSetA (and other sets in this work) are the following: the sequences of a file are said to be ''nonidentical'' if no two sequences in the file have a BLASTN hit of >95% identity over at least 95% of length of one of the sequences. The sequences of a target file are ''dissimilar'' to those of a reference file if no target sequence has a BLASTN hit against the reference file with an e-value smaller than 0.0001 over at least 40% of the length of the target sequence. These are relatively relaxed conditions that would still allow to survive for instance a full- length RNA together with a small hairpin (usually extracted from the Protein Data Bank) from that same molecule. The training set TrainSetA was created by merging all nonidentical sequences from all mentioned sources in this paper and then removing similar sequences between the sets. The processing of other data sets is similar to TrainSetA.
The data of TrainSetA / TestSetA do not contain family information, rather they are a pair of standard benchmark test sets, containing completely different sequences, but they belong to an RNA structure set[2, 6, 23-25]. TrainSetB and TestSetB are selected from the seed sequences of 22 RNA families [5.8S rRNA, spliceosomal RNAs (U1, U4), seven riboswitches, two ribozymes, nine cis-regulatory RNAs (such as Internal Ribosome Entry Sites, leader and frameshift RNAs), and bacteriophage pRNA], and the sequences of the two are completely different. DataSetA doesn't contain RNA family information, while each RNA of DataSetB includes RNA family information. Table 2 and Table 3 detail the datasets.
Details of TrainSetA (3166 Sequences, 48% base-paired, 0.1% non-canonical) and TestSetA (3166 Sequences, 48% base-paired, 0.1% non-canonical)
| RNA categories | Number (TrainSetA) | Number (TestSetA) |
|---|---|---|
| SSU/LSU domains | 1004 | 135 |
| tRNA | 157 | 140 |
| SRP RNA | 215 | 31 |
| RNaseP RNA | 150 | 29 |
| tmRNA | 266 | 63 |
| 5S RNA | 112 | 50 |
| group Ⅰ introns | 50 | 28 |
| group Ⅱ introns | 4 | 4 |
| telomerase RNA | 12 | 30 |
| <50 nts hairpins | 962 | 179 |
| other structures | 234 | 8 |
Details of TrainSetB (1094 Sequences, 46% base-paired, 4.8% non-canonical) and TestSetB (430 Sequences, 44% base-paired, 8.3% non-canonical)
| RNA categories | Number (TrainSetB) | Number (TestSetB) |
|---|---|---|
| 5.8S rRNA | 41 | 14 |
| U1 | 40 | 18 |
| U2 | 32 | 45 |
| 7 riboswitches | 365 | 233 |
| 2 ribozymes | 41 | 3 |
| 9 Cis regulatory RNAs | 575 | 116 |
| bacteriophage pRNAs | 0 | 1 |
Definition of Folding Rules
We define a folding rule as a specific SCFG (stochastic context-free grammar), containing the grammar model and probability parameters. The grammatical model is a set of grammatical rules describing the structural characteristics, and the probability parameters are the probability weights corresponding to these grammars. The tool, TORNADO, allows researchers to write grammatical rules to describe the various structural components of the RNA secondary structure, and as the literature details the specific structural rules that describe the structural features, this paper will not repeat them. The probability parameter of a folding rule is called a folding rule feature.
Extract Folding Rule Features
In a certain SCFG grammar model (e.g. g6 grammar[24]), a derivation corresponds to a specific secondary structure (semantically unambiguous), but for the same string, it can be generated by different derivations (syntactically ambiguous), so we can use the Cocke[26]-Younger[17]-Kasami[27] (CYK) algorithm, which is proposed by the three persons, to calculate the derivation with maximum probability of an RNA sequence in a given SCFG to build a unique syntax tree using the sequence and structure information.
We consider the probability ω(r) of the feature (the generation rule) r in a certain derivation as a parameter, and use generative training to train the parameters. The generative probabilistic model (G) specifies the joint probability of a given RNA sequence s and a structure πs:
P(s, πs | G) = ∏r∈P ω(r)Cr(s, πs)
The joint probability is a multiplication of each featural probability ω(r), wherein P is the set of all grammar rules, s represents the sequence, πs represents the structure, r represents the features (generation rules) and Cr (s, πs) is the count of feature r appearing in structure πs. Assuming that the model has only one nonterminal, the parameters of the model satisfy:
∑r∈P ω(r) = 1
This paper uses Maximum Likelihood Estimation (MLE) to train the generative probabilistic model, the logarithm sum of all the joint probabilities is optimized via a training set containing RNA sequences s and corresponding structures πs, and the Lagrange multiplier method is used to calculate:
∑s∈S ∑r∈P log(ω(r))Cr(s, πs) - λ(∑r∈P ω(r) - 1)
The closed-form solution can be obtained:
ω(r)* = ∑s∈S Cr(s, πs) / ∑s∈S ∑p∈P Cp(s, πs), " r∈P
We can get the values of all parameters ω(r) by counting the frequency of each feature r occurring in the training set. According to the generating training method, the occurrence frequency of each feature of the RNA can be obtained by counting the number of each rule in the grammar tree, so as to approximate the features of the rule. Each folding rule feature is the probability, so it can be vectorized. Fig. 10 shows the feature extraction flow chart (we choose the hairpin loop derivation of g6e grammar, S → L → aFu → aLSu → acSu → acLu → acgu, as an example).
Feature extraction flowchart.
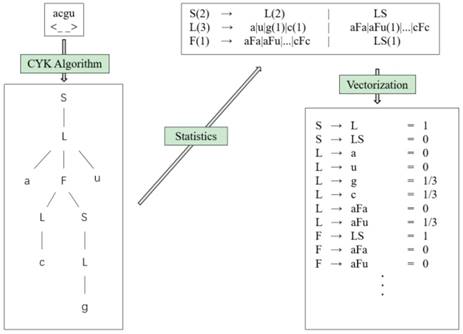
Using this process, we get the grammar tree from the sequence-structure information through the CYK algorithm, and obtain the frequencies of grammar rules via the generating training method. Finally, we can obtain the features of the folding rule.
Cluster Measurement Index - ARI
The most common measurement indexes include ARI (Adjusted Rand Index), NMI (Normalized Mutual Information), AC (Accuracy), and Purity. In this research, ARI is chosen as the index, because it measures the degree of coincidence of the two data distributions. We want to confirm the consistency between the diversity of folding rules and the difference in the RNA families, which is consistent with the function of the ARI.
ARI = (RI - E[RI]) / (max(RI) - E[RI])
ARI can yield negative values while RI only yields a value between 0 and +1. When the clustering effect is poor, ARI tends to zero, or even negative; when the clustering effect is very close to the reference class, ARI tends to 1. If the clustering effect is consistent with the reference class, ARI is 1.
Classification and Index
The inside-outside algorithm from which the inside variable e(i, j, N) and the outside variable f(i, j, N) can be calculated, was proposed by James K. Baker in 1979[28]. The inside algorithm (similar to the CYK algorithm) is used to calculate the probability of a SCFG generating a given string, and e(i, j, N) is the sum of the probabilities from all manners of nonterminal N generate sequences x¬i ... xj.
The inside algorithm gives the probability that G (a grammar model) generates ω (an RNA sequence):
Vinside(ω) =∑s∈S P(ω, s | G)
= P(ω | G)
P (Gi | ω) can be derived from the Bayesian formula:
P(Gi | ω) = P(ω | Gi)P(Gi) / P(ω)
P (ω | Gi) is Insidei (ω), P (Gi) is approximated by the proportion of Di in the total number of D. Therefore, L(ω) can be obtained:
P(Gi) ≈ |Di| / |D|
L(ω) = arg maxi∈[0,n] (Insidei(ω)P(Gi) / P(ω))
= arg maxi∈[0,n] Insidei(ω)P(Gi)
The classification correct rate is usually used as the evaluation index. The classification class L(ω) and the reference class Lref(ω) of each sample ω in the data are compared, and if they are the same, it is classified as correct, otherwise it is regarded as a misclassification. Then, the proportion of the samples with a correct classification in the total samples is counted.
Rcorrect =∑ω∈D1L(ω)=Lref(ω) / |D|
The reference class Lref(ω) is derived from the above clustering class, so only DataSetB containing family information is selected as the experimental data.
However, when the number of clusters is large, it is possible to divide RNAs with similar rules into different categories. In this case, if an RNA is assigned to a wrong category, and the difference between the classification category and the actual category is very small, it should not be directly regarded as an error classification. So, this paper presents another more reasonable evaluation index, classification approximation. This work uses cosine similarity to measure the similarity between folding rules. The cosine similarity takes each folding rule that contains m features as a vector in the m-dimensional space, and the similarity between the folding rules is obtained by calculating the angle between the folding rule eigenvectors.
The similarity degree matrix of the folding rules can be obtained:
By averaging all the elements of the similarity matrix, the average similarity of the data sets in a certain cluster number can be obtained. If the input RNA is randomly classified, its expected classification similarity is the average similarity, so it can be used as a baseline for analyzing the classification effect. For the classification class and the reference class (L (ω), Lref(ω)) of a certain RNA, the similarity can be obtained by accessing the value of the matrix directly. The classification similarity of the whole data can be obtained by averaging the classification similarity of all RNAs.
Rapprox =∑ω∈D sim(L(ω), Lref(ω)) / |D|
Improve the Prediction Accuracy
Parameter selection
In this paper, two kinds of parameters are used to select the appropriate folding rule parameters for the RNA sequence to be predicted.
Naive Classification
In the folding rule classification above, it is possible to assign a rule that best fits each of the RNAs to be predicted. The naive classification method uses a folding rule as a parameter for the prediction of RNA. After clustering the training data, folding rules are extracted for each class of Gi, and the Gi which makes P (Gi | ω) maximum is chosen as a parameter to predict ω:
gnaive(ω) = arg maxGi P(Gi | ω)
However, this method does not consider the information on other classes of the whole data, but simply gives the RNA to be predicted the folding rule corresponding to the category with the highest probability of generation. This method is called the naive classification method. It has a potential problem. As the number of clusters increases, the number of RNAs in each class decreases, and intra-class folding rules are easily biased due to too few samples.
Probability Weighting:
In order to consider the effect of all categories of folding rules, P (Gi | ω) is the weight, and we add all folding rules Gi together, that is, we calculate the conditional expectation of the folding rule when ω is known:
gnaive(ω) = Ε[G | ω]
=∑i Gi*P(Gi | ω)
P(Gi | ω) = P(Gi, ω) / P(ω)
= P(ω | Gi)P(Gi) / P(ω)
= P(ω | Gi)P(Gi) /∑i P(ω | Gi)P(Gi)
The obtained gexpect(ω) reflects the folding rule contribution of all RNAs in the entire training set to the RNA to be predicted. Folding rules with less probability of generation are given less weight, and are not completely ignored. When the production probabilities of two folding rules are similar, this method can effectively preserve the information of two folding rules at the same time.
Prediction methods
This paper uses the Maximum Expected Accuracy algorithm (MEA) to predict the secondary structure of RNA from the given parameters.
For a candidate structure s of an RNA sequence ω, the precision accuracy(s) is defined as the number of correctly predicted points in s. The idea of the MEA algorithm is to find the structure with the maximum expected accuracy.
smea = arg maxs∈S Ε[accuracy(s) | ω,G]
The whole process of prediction is shown in Fig. 11.
The pairing probability Pd(i, j) of two arbitrary base points of the RNA sequence can be calculated through the inside variable e(i, j, N) and the outside variable f(i, j, N). e(i, j, N) is the sum of the probabilities from all manner about nonterminal N generating the sequence x¬i ... xj, and f(i, j, N) is the sum of the probabilities from all manner about generating the remain sequence (x¬1 ... xi-1 and x¬j+1 ... xn) when N generates the sequence x¬i ... xj:
f(i, j, N) = P(S ⇒ x1…xi-1Nxj+1…xn)
The outside variable can be calculated through the outside algorithm.
After obtaining the inside variable and the outside variable, the pairing probability Pd(i, j) of two arbitrary base points can be calculated. For example, there are two generating rules that can generate pairing:
L → aFa | aFc | … | uFu
F → aFa | aFc | … | uFu
By summing the probabilities of the two rules analyzing xi…xj, the probability that sites i and j are paired can be obtained:
Pd(i, j) = f(i, j, N)*e(i+1, j-1, F)*P(L → xiFxj) / e(1, n, S) +
f(i, j, F)*e(i+1, j-1, F)*P(L → xiFxj) / e(1, n, S)
Prediction method flowchart
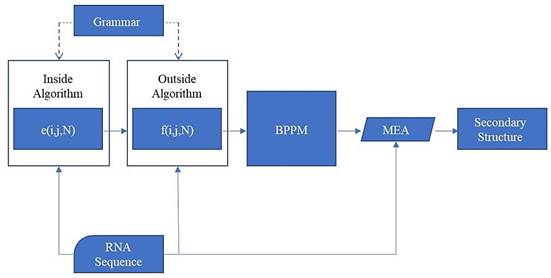
According to all the Pd(i, j) of the sequence, we can get the base-pairing probability matrix (BPPM):
The probability Ps(i) that any site i is not paired can be calculated from BPPM:
Ps(i) = 1 -∑j∈(1, n) Pd(i, j)
When the Pd(i, j) and the Ps(i) of all sites in the sequence are obtained, the MEA algorithm is used to search for the optimal secondary structure. The following recursive formula represents how to calculate the maximum expected accuracy Mi,j:
After the algorithm is finished, the maximum expected accuracy is M1,n, and the optimal structure is obtained by backtracking.
This paper is based on TORNADO (the most flexible and effective tool based on the statistical learning model)[29], which has been extended to the framework of "cluster-training-parameter selection-prediction". The improved prediction tool is called FocusFold. The experimental evaluation index is F-Score, which is used as a single metric and a comprehensive reflection of PRE (precision rate) and REC (recall rate).
Conclusions
We propose the feature of folding rules based on stochastic context-free grammar (SCFG). The diversity of RNA folding rules is confirmed by dimension reduction and cluster analysis, and the relationship between folding rules and family is also confirmed. also proposes the framework of RNA secondary structure prediction of "cluster-training-selection-prediction” and puts forward the probability-weighted method to select the appropriate parameter for the RNA to be predicted. Compared with TORNADO and RGRNA, FocusFold improves the prediction accuracy.
Due to the problem that folding diversity also exists in thermodynamic models, the difference in the folding rules proposed in this paper has value in improving the prediction accuracy of thermodynamics models. In addition, with the combination of high-throughput experimental data, the prediction accuracy of the thermodynamic model prediction method can be improved[30]. High-throughput experimental data can be also considered in the statistical learning model, as through high-throughput experimental data, we can obtain the chemical activity of each base site in the RNAs to be predicted, so that we can indirectly get the pairing probability of sites. If pairing probability is a constraint, the prediction accuracy may be further improved.
Author Contributions
ZhaoYang Xie, Min Zhu and Yu Zhu conceived and designed the experiments; ZhaoYang Xie and YiZhou Li performed the experiments; Yu Zhu and ZhaoYang Xie analyzed the data; Yu Zhu wrote the paper; Min Zhu and Yi-Ping Phoebe Chen reviewed and edited the manuscript. All authors read and approved the manuscript.
Competing Interests
The authors have declared that no competing interest exists.
References
1. Tsang HH, Wiese KC. A permutation based simulated annealing algorithm to predict pseudoknotted RNA secondary structures. Int J Bioinform Res Appl. 2015;11:375-96
2. Andronescu M, Condon A, Hoos HH, Mathews DH, Murphy KP. Efficient parameter estimation for RNA secondary structure prediction. Bioinformatics. 2007;23:i19
3. Chiu JKH, Chen YPP. Efficient Conversion of RNA Pseudoknots to Knot-Free Structures Using a Graphical Model. IEEE Transactions on Biomedical Engineering. 2015;62:1265-71
4. Goertzen LR, Cannone JJ, Gutell RR, Jansen RK. ITS secondary structure derived from comparative analysis: implications for sequence alignment and phylogeny of the Asteraceae. Molecular Phylogenetics & Evolution. 2003;29:216-34
5. Zuker M, Sankoff D. RNA secondary structures and their prediction. Bulletin of Mathematical Biology. 1984;46:591-621
6. Zhi JL, Gloor JW, Mathews DH. Improved RNA secondary structure prediction by maximizing expected pair accuracy. Rna-a Publication of the Rna Society. 2009;15:1805-13
7. Doshi KJ, Cannone JJ, Cobaugh CW, Gutell RR. Evaluation of the suitability of free-energy minimization using nearest-neighbor energy parameters for RNA secondary structure prediction. Bmc Bioinformatics. 2004;5:1-22
8. Gardner PP, Giegerich R. A comprehensive comparison of comparative RNA structure prediction approaches. Bmc Bioinformatics. 2004;5:1-18
9. Yonemoto H, Asai K, Hamada M. A semi-supervised learning approach for RNA secondary structure prediction. Computational Biology & Chemistry. 2015;57:72-9
10. Eddy SR, Durbin R. RNA sequence analysis using covariance models. Nucleic Acids Research. 1994;22:2079-88
11. Knudsen B, Hein J. Pfold: RNA secondary structure prediction using stochastic context-free grammars. Nucleic Acids Research. 2003;31:3423-8
12. Rivas E, Lang R, Eddy SR. A range of complex probabilistic models for RNA secondary structure prediction that includes the nearest-neighbor model and more. Rna-a Publication of the Rna Society. 2012;18:193-212
13. Gorban AN, Kégl B, Wunsch DC, Zinovyev AY. Principal Manifolds for Data Visualization and Dimension Reduction: Springer Berlin Heidelberg. 2008.
14. Yang H, Tang H, Chen XX, Zhang CJ, Zhu PP, Ding H. et al. Identification of Secretory Proteins in Mycobacterium tuberculosis Using Pseudo Amino Acid Composition. BioMed Research International,2016, (2016-8-11). 2016;2016:5413903
15. Lai HY, Chen XX, Chen W, Tang H, Lin H. Sequence-based predictive modeling to identify cancerlectins. Oncotarget. 2017;8:28169-75
16. Lin H, Liang ZY, Tang H, Chen W. Identifying sigma70 promoters with novel pseudo nucleotide composition. IEEE/ACM Transactions on Computational Biology & Bioinformatics. 2017
17. Younger DH. Recognition and parsing of context-free languages in time n 3 *. Information & Control. 1967;10:189-208
18. Jin L, Xu C, Hong L, Wang C, Ying W, Luan K. et al. RGRNA: prediction of RNA secondary structure based on replacement and growth of stems. Computer Methods in Biomechanics & Biomedical Engineering. 2017;20:1-12
19. He B, Chai G, Duan Y, Yan Z, Qiu L, Zhang H. et al. BDB: biopanning data bank. Nucleic Acids Research. 2016;44:D1127-D32
20. Liang ZY, Lai HY, Yang H, Zhang CJ, Yang H, Wei HH. et al. Pro54DB: a database for experimentally verified sigma-54 promoters. Bioinformatics. 2017;33:467-9
21. J H, B R, P Z, F N, J Y, X W. et al. MimoDB 2.0: a mimotope database and beyond. Nucleic Acids Research. 2012;40:271-7
22. Wei C, Hua T, Hao L. MethyRNA: a web server for identification of N6-methyladenosine sites. Journal of Biomolecular Structure & Dynamics. 2016;35:1
23. Do CB, Woods DA, Batzoglou S. CONTRAfold: RNA secondary structure prediction without physics-based models. Bioinformatics. 2006;22:e90
24. Dowell RD, Eddy SR. Evaluation of several lightweight stochastic context-free grammars for RNA secondary structure prediction. Bmc Bioinformatics. 2004;5:71
25. Andronescu M, Condon A, Hoos HH, Mathews DH, Murphy KP. Computational approaches for RNA energy parameter estimation. Rna-a Publication of the Rna Society. 2010;16:2304
26. Cocke J. Programming languages and their compilers: preliminary notes: Courant Institute of Mathematical Sciences. New York University. 1970
27. Kasami T. An Efficient Recognition and Syntax-Analysis Algorithm for Context-Free Languages. Technical Report Air Force Cambridge Research Lab. 1966
28. Baker JK. Trainable grammars for speech recognition. Speech Communication Papers for the Meeting of the Acoustical Society of America. 1979;65:547-50
29. Rivas E. The four ingredients of single-sequence RNA secondary structure prediction. A unifying perspective. Rna Biology. 2013;10:1185
30. Wu Y, Shi B, Ding X, Liu T, Hu X, Yip KY. et al. Improved prediction of RNA secondary structure by integrating the free energy model with restraints derived from experimental probing data. Nucleic Acids Research. 2015;43:7247-59
Author contact
![]() Corresponding authors: Min Zhu and Yi-Ping Phoebe Chen
Corresponding authors: Min Zhu and Yi-Ping Phoebe Chen

 Global reach, higher impact
Global reach, higher impact