PDF

Int J Biol Sci 2011; 7(1):112-132. doi:10.7150/ijbs.7.112 This issue Cite

Review

Finite Element Method (FEM), Mechanobiology and Biomimetic Scaffolds in Bone Tissue Engineering

A. Boccaccio¹ , A. Ballini² , C. Pappalettere¹, D. Tullo², S. Cantore², A. Desiate²

1. Dipartimento di Ingegneria Meccanica e Gestionale, Politecnico di Bari, 70126, Bari, Italy
2. Department of Dental Sciences and Surgery, Faculty of Medicine and Surgery, University of Bari “Aldo Moro”, Bari, Italy

✉ Corresponding author: Dr. Antonio Boccaccio, Dipartimento di Ingegneria Meccanica e Gestionale, Politecnico di Bari, Viale Japigia, 182, 70126, Bari, Italy. Tel: +39-080-5962829; Fax: +39-080-5962777; Email: a.boccaccioit. Dr. Andrea Ballini, Department of Dental Sciences and Surgery, University of Bari “Aldo Moro”, Piazza Giulio,Cesare, 11, 70124, Bari, Italy. Tel: +39-080-5594242; Fax: +39 080 5478043; Email: andrea.balliniuniba.it More

Abstract

Techniques of bone reconstructive surgery are largely based on conventional, non-cell-based therapies that rely on the use of durable materials from outside the patient's body. In contrast to conventional materials, bone tissue engineering is an interdisciplinary field that applies the principles of engineering and life sciences towards the development of biological substitutes that restore, maintain, or improve bone tissue function. Bone tissue engineering has led to great expectations for clinical surgery or various diseases that cannot be solved with traditional devices. For example, critical-sized defects in bone, whether induced by primary tumor resection, trauma, or selective surgery have in many cases presented insurmountable challenges to the current gold standard treatment for bone repair. The primary purpose of bone tissue engineering is to apply engineering principles to incite and promote the natural healing process of bone which does not occur in critical-sized defects. The total market for bone tissue regeneration and repair was valued at $1.1 billion in 2007 and is projected to increase to nearly $1.6 billion by 2014.

Usually, temporary biomimetic scaffolds are utilized for accommodating cell growth and bone tissue genesis. The scaffold has to promote biological processes such as the production of extra-cellular matrix and vascularisation, furthermore the scaffold has to withstand the mechanical loads acting on it and to transfer them to the natural tissues located in the vicinity. The design of a scaffold for the guided regeneration of a bony tissue requires a multidisciplinary approach. Finite element method and mechanobiology can be used in an integrated approach to find the optimal parameters governing bone scaffold performance.

In this paper, a review of the studies that through a combined use of finite element method and mechano-regulation algorithms described the possible patterns of tissue differentiation in biomimetic scaffolds for bone tissue engineering is given. Firstly, the generalities of the finite element method of structural analysis are outlined; second, the issues related to the generation of a finite element model of a given anatomical site or of a bone scaffold are discussed; thirdly, the principles on which mechanobiology is based, the principal theories as well as the main applications of mechano-regulation models in bone tissue engineering are described; finally, the limitations of the mechanobiological models and the future perspectives are indicated.

Keywords: Finite Element Analysis, Mechanobiology, Bone Tissue Engineering, Scaffold, Mechano-regulation Algorithms.

Introduction

Bone tissue engineering is the general term for a number of ways by which bony tissue lost as a result of trauma and disease might be restored. It is possible to use cells alone (as in the case of bone marrow transplantation), however for most applications in regenerative medicine, cells in combination with appropriate scaffolds and carriers are more commonly used [1]. Traditionally, bone tissue engineering consists of harvesting cells from a patient, expanding them in vitro and culturing them into a biomaterial -also called a scaffold- that serves as a structural framework to allow cell attachment, proliferation and differentiation into a controlled phenotype [2].

Among the disciplines involved in the designing of new scaffolds for bone tissue engineering mechanobiology certainly plays a crucial role. Mechanobiology merges the older science of mechanics with the newer and emerging fields of research of molecular biology and genetics. At the center of mechanobiology is the cellular process of mechano-transduction, or the way by which the cells sense and respond to mechanical forces or, in general to biophysical stimuli. Experimental and analytical models are often integrated in mechanobiology to gain a deeper understanding of the cells' response to mechanical factors. The purpose of computational mechanobiology is to determine the quantitative rules that govern the effects of mechanical loading on tissue differentiation, growth, adaptation and maintenance [3]. Experiments provide insights and measurements, which can then be interpreted within the context of analytical frameworks. Analytical simulations permit investigation of possible explanations that require in vivo validation and will suggest further experimental investigations.

Different experimental studies demonstrated that the cell culture conditions have a significant impact not only on the cell morphology, such as the extent of cell attachment and ingrowth, but also on cellular activities [4-8] thus suggesting that interactions with the local mechanical environment should be considered in the design of constructs for functional bone/cartilage repair. Computational mechano-biological models can be utilized to predict the possible patterns of the tissues differentiating within scaffolds and then to determine the optimal parameters governing scaffold performance. An example of controllable design parameter for a scaffold is represented by its porosity which should: (i) facilitate the migration and proliferation of precursor cells and (ii) provide an appropriate microenvironment for cell proliferation and differentiation. The conflicting nature of the requirements was described by Karageorgiou and Kaplan [9] who found that higher porosities result in greater bone ingrowth in vivo but that porosity cannot increase indefinitely as the structural integrity of the scaffold must be preserved. In the case of biodegradable scaffolds, the determination of the optimal porosity is a more complex task. For such scaffolds, two different processes occur simultaneously: the dissolution and the differentiation of the tissues. The first process determines a decrease of the scaffold stiffness, the second one, if a favourable biophysical stimulus is elicited (by the boundary and loading conditions acting on the scaffold) leads to an increasing stiffness of the global system scaffold/tissues. Computational mechano-regulation models can then be used to determine how the scaffold porosity and the structural response of the scaffold change over time. Such models can predict the evolution in time of the dynamic equilibrium between dissolution and tissue differentiation process thus allowing to determine the optimal value of initial porosity that the scaffold should possess before the degradation process initiates.

A possible strategy that can be adopted to determine the structural response of a biomemetic scaffold and hence the stimulus acting on the regenerate is the finite element method (FEM) which allows the investigator to evaluate the field of stress and strain within both, the scaffold structure and the mesenchymal tissue.

This article will review the computational studies reported in literature that through a combined use of the finite element method and mechano-regulation algorithms described the possible patterns of tissue differentiation in biomimetic scaffolds for bone tissue engineering. Given the volume of work in this field it is not possible to be comprehensive but it is possible to describe some current research and to highlight future research directions that may be relevant to regenerative medicine.

Finite Element Method (FEM)

Generalities

The Finite Element Method (FEM) is a numerical technique which gives approximate solutions to partial differential equations (PDE) that model problems arising in physics and engineering, as well as of integral equations. The solution approach is based either on eliminating the differential equation completely (steady state problems), or rendering the PDE into an approximating system of ordinary differential equations, which are then numerically integrated using standard techniques such as Euler's method, Runge-Kutta, etc [10].

As in simple finite difference schemes, FEM requires a problem defined in geometrical space (or domain) to be subdivided into a finite number of smaller regions. For this purpose, the body under analysis must be discretized in many sub-domains that are denoted as elements. If the body's geometry is complicated, the elements are usually shaped as tetrahedra. Each element includes a certain number of vertices called nodes. The assembly of elements and nodes is called the finite element mesh.

Loads acting on the body are modelled as forces applied to nodes. The constraints are modelled by preventing the nodal displacements along the directions where each constraint acts. Loads and constraints are indicated as boundary conditions. Consider a single element: the forces and displacements at the nodes are related by the stiffness matrix for the element, denoted [K^e]. Each element has nodes which join with the nodes on adjacent elements to re-create the total structure. The stiffness term for a node is then the addition of all the stiffness terms from the elements joined at that node. The stiffness matrix for the whole structure (denoted [K]) can be obtained by re-assembly of the individual elements. If there are n nodes in a three-dimensional finite element model, then [K] will be a 3n × 3n matrix and an equation of the form:

 (1) 

can be used to relate all nodal forces {F} and nodal displacements {δ}. The forces in each node are zero, except for the nodes where the load is applied. Knowing this, the entries can be inserted into {F}, and equation (1) can be solved for {δ} to obtain the complete set of nodal displacements. Partial derivatives of each displacement component are then computed and combined to obtain deformations. Finally, stresses are computed by using constitutive equations that put into relationship deformations and stresses.

This powerful design tool has significantly improved both the standard of engineering designs and the methodology of the design process in many biomedical applications [11-12]. In three principal areas of biomechanics the FEM has found a large use: (i) analysis of the skeleton; (ii) analysis and design of orthopedic devices and (iii) analysis of tissue growth, remodelling and degeneration. The method, applied to bone and soft tissue has allowed researchers to predict the deformations of musculoskeletal structures and to explore biophysical stimuli within tissues at the cellular level. Incorporating finite element models into iterative computer procedures, adaptive biological processes have been simulated opening an exciting field of research by allowing scientists to test proposed rules or algorithms for tissue growth, adaptation and degeneration. These algorithms have been used to explore the mechanical basis of processes such as bone remodelling, fracture healing and osteoporosis.

Generation of the Finite Element Model

A critical issue encountered in finite element modelling is the generation of the finite element model. While in other engineering applications, the model is typically built in Computer Aided Design (CAD) environment and then imported into the finite element software (where it is discretized into finite elements), in biomedical engineering a different approach is adopted. The introduction of imaging techniques [13, 14] (such as Computerized Tomography (CT), Micro-Computed Tomography (micro-CT) and Nuclear Magnetic Resonance (NMR)) and the development of software interfaces that allow medical image scans to be converted into CAD data solved the problem of generating the finite element model of anatomical sites. In general, CAD models can be generated from CT, micro-CT or NMR scans by following two distinct approaches: “geometry based” (GB) and “voxel based” (VB). The former method defines a geometric model comprised of curves and surfaces that is finally discretized into finite elements [15, 16]. The strength point of the geometry based approach is the possibility of creating smooth surfaces and hence to simulate any kind of interface. For instance, GB has been successfully applied by some of the present authors to the analysis of a simplified model of bone-implant interface [17]. Procedures for reconstructing a model of the femur and pelvis requiring minimum amount of patient data as feasible have been presented in literature [18]. The same GB approach has been followed for example by Gao and Ding [19] and Boccaccio et al. [20-22] in generating finite element meshes of complicated models of dental biomechanics. The voxel based approach is more diffused than the geometry based approach and relies on the principle that each group of voxels (the base unit of 3-D imaging) is directly converted into hexahedral elements [15, 23, 24]. The procedure seems to be effective for modelling microscopic structures such as, for instance, trabecular bone volumes [25-28]. However, the presence of “ramp effects” in the reconstructed contour surfaces makes it very difficult to simulate the actual behaviour of bone-implant interfaces [29]. Contact problems can be solved with VB only by adopting smoothing techniques [30, 31] where interaction with the user is however required. Evaluations of the errors made in reconstructing finite element models from medical image scans have been carried out by Charras and Guldberg [32] for the VB approach and by Boccaccio et al. [33] for the GB approach.

The imaging technique mainly utilized in bone tissue engineering is the micro-CT. This technique is based on the biomaterial being scanned through X-rays crossing the material as the sample rotates within the X-ray beam. A three-dimensional volume is reconstructed from this set of data using filtered back projection [34]. The resolution that can be obtained using such a technique depends on the X-ray source and detector, in combination with the field of view chosen [35, 36]. The micro-CT technique has been used, in tissue engineering, for different purposes: to characterize scaffolds [37]; to monitor three-dimensional mineralization over time in a perfusion bioreactor [38]; to evaluate scaffold/tissue integration, tissue formation and scaffold degradation [39]. Utilizing micro-CT data, Lacroix et al. [40] developed finite element models of various bone scaffolds based on calcium phosphate in order to calculate the load transfer from the biomaterial structure to the biological entities. Sandino et al. [41], by adopting this same imaging technique built a very complex model of a scaffold for bone tissue engineering and by means of the finite element method analyzed the behaviour of the mechanical stimuli within some calcium phosphate-based scaffolds in terms of stress and strain distributions in the solid material phase and fluid velocity, fluid pressure and fluid shear stress distributions in the pores filled of fluid. The principal limitation of this technique is represented by the fact that while the traditional CT machine can be used for the scanning of any anatomical region, the micro-CT technique can reconstruct the morphology of the tissues of only a few peripheral anatomical sites or that of small samples or scaffolds [42].

Mechanobiology

Basic Principles

Growth, adaptation, and remodelling of tissues are caused by processes active inside the tissue. These processes are executed by cells. They involve changing the tissue from one phenotype to another, or by replacing it altogether; either way a new cell population becomes resident at the place where differentiation has occurred. One cell type that plays a crucial role in such processes is the stem cell. Recently researchers have attempted to elucidate what controls stem cell differentiation. It has been suggested that chemical and mechanical stimuli can control the differentiation of adult skeletal stem cells (also called mesenchymal stem cells) into either fibrous connective tissue, cartilaginous tissue, bone, or adipose tissue [43, 44]. The experiments conducted on cells (micropipette aspiration [45], atomic force microscopy [46]) show unequivocally that mechanical stressing elicits expression of signalling and matrix molecules. These experiments have shown that the magnitude of stimuli acting due to physiological mechanical loading can cause cells to signal with Nitric Oxide (NO) and prostaglandin E₂ (PGE₂) molecules [47]. Objective of the mechanobiology is the study of the relationship between mechanical stressing on undifferentiated tissue and the ultimate tissue phenotype formed.

Cell differentiation is first encountered in the embryo when the blastema cells differentiate into specialized cell types. In the process of the development of the embryo, soft connective tissues form first and following this bone forms directly from the fibrous tissue (intramembranous ossification) or by replacing the cartilage (endochondral ossification) [48]. Tissue differentiation is also observed in the adult. The typical process where tissue differentiation is readily apparent is in fracture healing. There are two ways for fractures to heal: by primary fracture healing or by secondary fracture healing. Primary healing involves a direct attempt by the cortex to re-establish itself once it has become interrupted. When stabilisation is not adequate to permit primary healing, the abundant capillaries required for bone repair are constantly ruptured and secondary healing takes place. Secondary healing involves responses within the periosteum and external soft tissues and subsequent formation of an external callus. Secondary fracture healing occurs in the following stages. Blood emanates from the ruptured vessels and a haemorrhage quickly fills the fracture gap space. Macrophages remove the dead tissue and generate initial granulation tissue for the migration of undifferentiated mesenchymal stem cells, originating an initial stabilizing callus. These cells proliferate and migrate from the surrounding soft tissue [49-52]. In the next stage, mesenchymal cells may differentiate into chondrocytes, osteoblasts or fibroblasts (Fig. 1), depending on the biological and mechanical conditions. These differentiated cells begin to synthesize the extracellular matrix of their corresponding tissue [53]. Intramembranous woven bone is produced by direct differentiation of the stem cells into osteoblasts. Endochondral ossification occurs when chondrocytes are replaced by osteoblasts.

One of the most important applications of mechanobiology is in the development of new clinical therapies, for example in bone fracture healing, distraction osteogenesis or osteoporosis, as well as in the improvement of implant design. With implants such as prostheses, cells migrate up to the implant surface and begin to synthesis matrix, but if the micromotion is too high bone will not form to stabilise the implant - instead a soft tissue layer will form [54, 55]. Another important domain of applicability is in bone tissue engineering and regenerative medicine. Appropriate biophysical stimuli are needed in bone scaffolds, in addition to nutrients and appropriate levels of oxygen supply, to favour an appropriate tissue differentiation process [56, 57]. It appears rather clear that bioengineers have many reasons to be interested in computational models of tissue differentiation. The very large number of variables involved in bone tissue engineering (scaffold properties, cells seeding, in vitro conditioning, and post-implantation loading environments) makes computer simulation a condicio sine qua non for any rational design process based on engineering principles.

Mechanobiology problems can be split into two parts:

1. solution of problem to determine deformations at the cellular and sub-cellular level when the forces on the organ (e.g. whole bone) are known. This involves determination of constitutive models of the tissues so as organ-to-tissue computations can be performed, and it requires micro/nano-mechanical modelling to perform the tissue-to-cell and the cell-to-sub-cellular component computations. At the cellular length scales mechanobiology can explain how the cells sense input signals from the environment and how their response can induce different cellular behaviours such as growth, differentiation, apoptosis, migration, gene expression and signal transduction; these signals are of different nature and may be classified into mechanical [58-61], topographical [58, 62-64] and chemical [65, 66] cues. At the sub-cellular length scales mechanobiology can have a substantial mechanistic affect on shaping nuclear, cytoskeletal, and cellular arrangements and function [67-72].
2. derivation of equations to relate the mechanical stimuli to adaptation of the tissue/organ construct.

This review will focus on the aspect (2).

 Figure 1 

The mesengenic process. Reprinted from [43] Clinics in Plastic Surgery, Vol. 21, Issue 3, Caplan AI, The mesengenic process, Pages No. 429-435, Copyright (1994) with permission from Elsevier.

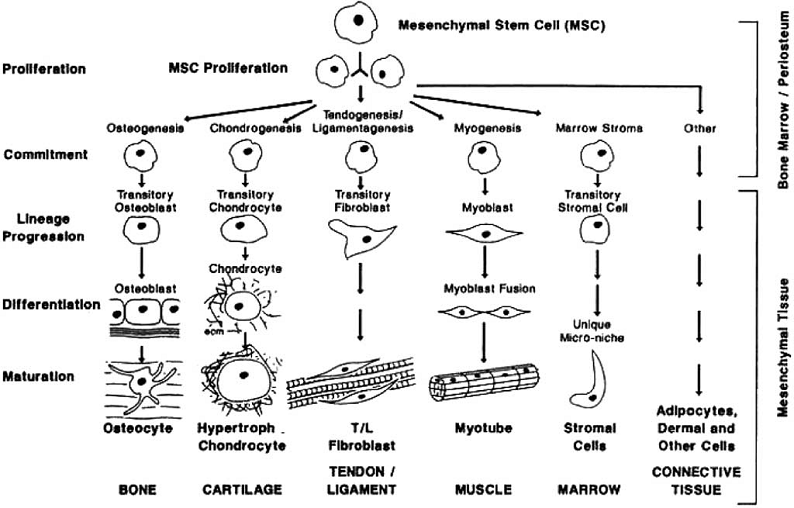
Mechanobiology of stem cells

Mesenchymal stem cells (MSCs) are nonhematopoietic progenitor cells found in adult tissues. They posses an extensive proliferative ability in an uncommitted state and hold the potential to differentiate along various lineages of mesenchymal origin in response to appropriate stimuli [73]. Bone marrow is the most important source for MSCs [50, 74-78]. MSCs have been also identified in different other tissues such as adipose, periosteum, trabecular bone, synovium, skeletal muscle, dental pulp and periodontal ligament [79-82]. The stem cells in these locations lie dormant in a non-proliferating state until they are required to participate in local repair and regeneration. Quiescent MSCs become mobilised during repair and remodelling through regulation by external chemical and physical signals that control their activation, proliferation, migration, differentiation and survival i.e. their fate [83, 84].

Theories on the relationship between mechanics and biology were originally proposed in relation to fracture healing. These theories later evolved into 'mechano-regulation algorithms'; a finite set of rules that govern the effects of mechanical loading on stem cells and tissues. One key aspect in these algorithms is the modelling of the cellular processes such as the cellular dispersal, the proliferation, the apoptosis, etc.

Concerning the process of cellular dispersal, it has been suggested that the movement of cells can be thought of as an assemblage of particles, with each particle moving around in a random way [85]. In many studies [86-90], a diffusion equation of the form:

 (2) 

being c the concentration of stem cells in a given volume and D the diffusion coefficient, has been used to simulate the movement of cells through regenerating tissues. Gruler and Bültmann [91] measured a diffusion coefficient of 240 μm²/min for the movement of leukocytes. Bailón-Plaza and van der Meulen [92] developed a mathematical model of fracture healing and found that the diffusion coefficient representative of the movement of stem cells should be higher than the value above described since in vitro substrate conditions may slow down cellular migration and growth factors released during fracture healing act as chemoattractants to increase cell speeds in vivo [93]. However the model of cellular dispersal adopted in these studies [86-90] presents the limitation that the diffusion coefficient was assumed to be independent of the tissue differentiation process. In other words, the diffusion coefficient was set the same regardless of the cell phenotype or the tissue through which the cell was moving. Furthermore, this approach implicitly assumes that cells attempt to achieve a homogenous population density within the area of analysis. In order to accurately simulate the tissue differentiation process, Lacroix et al. [94] hypothesised that the processes of cellular mitosis and apoptosis (programmed cell death) should be taken into account. Therefore, the rate of change in cell concentration assumes the form:

 (3) 

The first term on the fight-hand side of equation (3) describes cell migration by simple linear diffusion; the second term describes cell mitosis, where c_c(x,t) is the chemical concentration of a mitosis-inducing factor; s(c_c) is a function describing the mitosis rate per cell; and k is a constant describing the cell death or removal rate [95]. Since the mesenchymal stem cells can differentiate into cells of different phenotypes i (i.e. fibroblasts, chondrocytes and osteoblasts) that produce different tissues j (i.e. fibrous tissue, cartilage and bone), a logical progression of the idea proposed by Lacroix et al., [94] would be that the diffusion coefficient D would depend on the cell phenotype i and the tissue type j through which the cell is moving. This modelling of the cellular dispersal has been adopted in Kelly and Prendergast [96, 97]. Following an extensive review of the literature [98-106] on mechano-regulated mitosis, Kelly and Prendergast discovered that relatively high magnitudes of strain were seen to increase cellular proliferation, while very high magnitudes of stress or strain resulted in cell death [93]. In a study of osteochondral defect repair, they assumed a quadratic relationship between cell proliferation/death and octahedral shear strain. Boccaccio et al. [89, 90], modelled the cellular dispersal by using the diffusion equation (2) however, in order to better describe the time evolution of the healing process of a fracture callus, they assumed that the Young's modulus of all tissues within the callus increases exponentially with time. The equation describing the variation of the Young's modulus is of the form:

 (4) 

where E_i represents the Young's modulus for tissue phenotype i (where i is either fibrous tissue, cartilage, immature or mature bone), t is the time and K_i and γ_i are two parameters regulating the shape of the exponential curve. The choice of an exponential law was based on the results of Richardson et al. [107] who observed an exponential increase in stiffness during tibial fracture healing. This approach accounts for the fact that MSCs not only require time to differentiate, but that the differentiated cell types require time to synthesise and remodel new tissue.

Despite its convenience to model, diffusion is not the mechanism of cell dispersal; instead cells disperse by crawling or proliferation or are transported in a moving fluid [57]. In order to better simulate the cellular processes Pérez and Prendergast [108] developed a 'random-walk' model to describe cell proliferation and migration, with and without a preferred direction. In this approach, a regular lattice of points is superimposed on the fracture domain. Each lattice point is either empty, or occupied by a stem cell. Cell movement can be simulated by moving a cell from one lattice point to another; cell proliferation, by dividing a cell so that the daughter cell takes up a neighbouring lattice point; cell apoptosis, by removing a cell at a lattice point. The same lattice-based modelling approach has been adopted by Checa and Prendergast [109] to develop a mechano-regulation algorithm including angiogenesis. Angiogenesis has been simulated by linking endothelial cells to form “capillaries” within the lattice.

Principal Theories

Comparing patterns of differentiation during tissue repair to predictions of the mechanical environment within the mesenchymal tissue has led to the development of a number of hypothesis for mechano-regulated tissue differentiation. Pauwels [110], who was the first to propose such a hypothesis, suggested that precursor mesenchymal stem cells (MSCs) differentiate according to the following rules: “(1) hydrostatic pressure stimulates MSC differentiation into chondrocytes to form cartilage, shearing stimulates MSC differentiation into fibroblasts to form fibrous connective tissue, combinations of the two stimulate fibrocartilage formation (as in discs and menisci), and (2) only when a soft tissue has stabilized the environment is MSC differentiation into osteoblasts favoured leading to the formation of bone”.

Pauwels combined these two rules diagrammatically (Fig. 2) to illustrate his idea that the formation of either fibrous connective tissue or cartilaginous tissue was required to stabilize the mechanical environment before ossification could occur.

 Figure 2 

Pauwels' diagram encapsulating his hypotheses with respect to how mechanical forces regulate tissue differentiation and ossification. Reprinted from [111] Bone, Vol. 19, Issue 2, Weinans H, Prendergast PJ, Tissue adaptation as a dynamical process far from equilibrium, Pages No. 143-149, Copyright (1996) with permission from Elsevier.

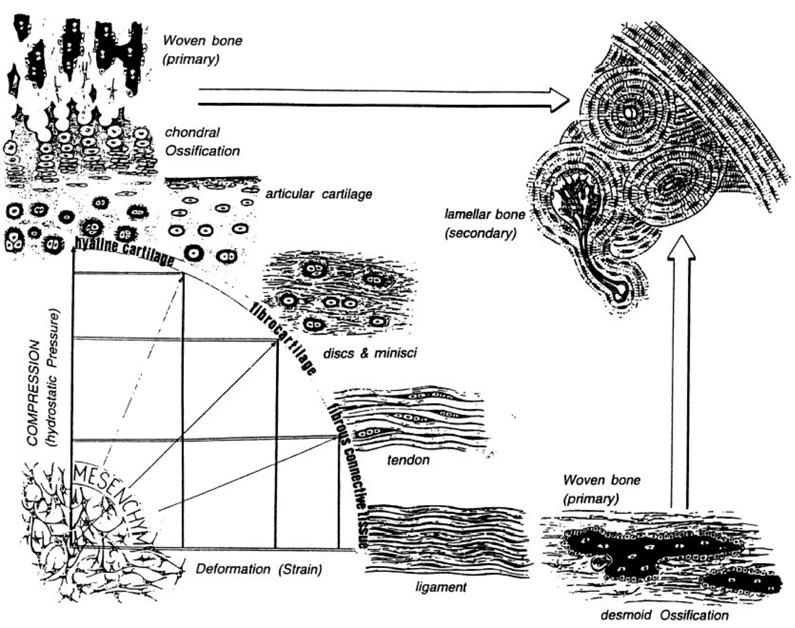
The rule (1) informs what appears on the x axis (deformation by shear strain) and the y axis (hydrostatic pressure). A combination of these two biophysical stimuli will act on the mesenchymal cell pool leading to either hyaline cartilage, fibrocartilage or fibrous tissue as represented on the perimeter of the quadrant. The larger arrows indicate that, as time passes, ossification of these soft tissues occurs, but may be inhibited, or at least slowed down according to rule (2).

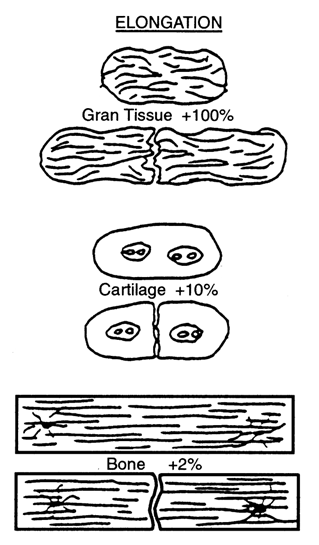
Based on a qualitative analysis of clinical results of fracture healing, Perren [112], and Perren and Cordey [113] proposed that tissue differentiation is controlled by the tolerance of various tissues to strain. The basis of this theory, - normally known as 'the interfragmentary strain theory' - is that a tissue that ruptures or fails at a certain strain level cannot be formed in a region experiencing strains greater than this level. Perren [112] first showed that, due to a difference in strength and rigidity between tissues, the tolerance to elongation is very different. For example, lamellar bone would rupture under a strain of 2 %, cartilage would rupture for a strain of about 10 % whereas granulation tissue can withstand strains up to 100 % (Fig. 3). Due to this different tolerance to rupture, healing occurs by a progressive tissue differentiation from the initial granulation tissue, to fibrous tissue, cartilaginous tissue and then bony tissue.

Carter and colleagues [114, 115] assumed that the intermittent or cyclic stresses and the vascularity in the early callus are the major local factors to be considered in the fracture healing process. In the early callus material (a) fracture elicits an osteogenic stimulus; (b) if minimal cyclic stresses (or strains) are created and there is a good blood supply, bone will form; (c) high stress magnitudes will encourage tissue proliferation; (d) high shear and/or tensile hydrostatic stresses encourage fibrous tissue formation; (e) high compressive hydrostatic stresses encourage chondrogenesis; and (f) if cartilage of fibrocartilage forms, cyclic shear will promote and compressive hydrostatic stresses inhibit endochondral ossification (Fig. 4).

 Figure 3 

Interfragmentary Strain Theory: A tissue cannot exist in an environment where the interfragmentary strain exceeds the strain tolerance of the extracellular matrix of the tissue. Reprinted from [112] Current Orthopaedic Practice -- A Review and Research Journal, Clinical Orthopaedics and Related Research, Vol. 138, Perren S, Physical and Biological Aspects of Fracture Healing with Special Reference to Internal Fixation, Pages No. 175-196, Copyright (1979) with permission from Wolters Kluwer Health.

 Figure 4 

Hypotheses of Carter et al. [115] for the influence of intermittent stresses and vascularity on differentiation of mesenchymal tissue. Reprinted from [115] Journal of Orthopaedic Research, Vol. 6, Issue 5, Carter DR, Blenman PR, Beaupré GS, Correlations between mechanical stress history and tissue differentiation in initial fracture healing, Pages No. 736-748, Copyright (1988) with permission from John Wiley and Sons.

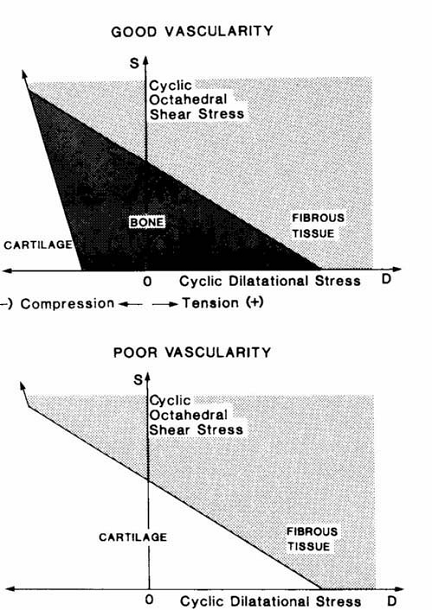
If, however, for some reason there is poor vascularization of the tissue, bone cannot form and a small, fibrocartilaginous callus may result (Fig. 4). Carter et al. [115] summarized the severity of the cyclic stress state in terms of two stress invariants, the octahedral shear stress S and the hydrostatic or dilatational stress D defined as:

 (5) 

where σ₁, σ₂ and σ₃ are the peak cyclic principal stresses. To calculate an index reflecting the tendency for ossification, the loading history over some period of time (e.g., an “average” day) was summarized in terms of c loading cases. The net stimulus for ossification was expressed as an osteogenic index I that is calculated as:

 (6) 

where the subscript i indicates a specific loading case, n_i = number of loading cycles, S_i = cyclic octahedral shear stress, D_i = cyclic hydrostatic (dilatational) stress, and k = empirical constant to be determined.

Claes and Hiegele [116] presented a new quantitative tissue differentiation theory which relates the local tissue formation in a fracture gap to the local stress and strain. Their hypothesis was that the amounts of strain and hydrostatic pressure along existing calcified surfaces in the fracture callus determine the differentiation of the callus tissue (Fig. 5).

 Figure 5 

Rule of tissue differentiation relating mechanical stimuli to tissue types hypothesized by Claes and Heigele [116].

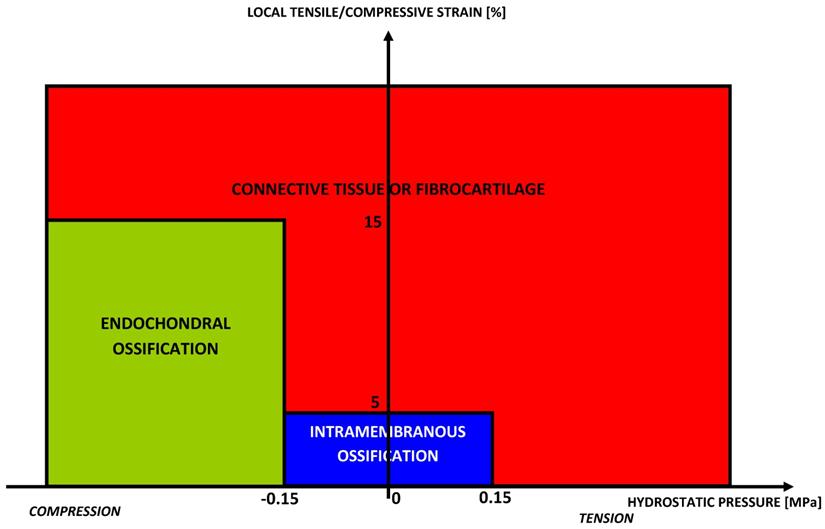
The authors compared the local strains and stresses in the callus as calculated from a finite element model with histological findings from an animal fracture model. The formulated hypothesis predicted intramembranous bone formation for strains smaller approximately ±5% and hydrostatic pressures smaller than ±0.15 MPa. Endochondral ossification was associated with compressive pressures larger than about -0.15 MPa and strains smaller than ±15%. All other conditions seemed to lead to connective tissue or fibrous cartilage.

Kuiper et al. [117-119] developed a differentiation tissue theory using the tissue shear strain and fluid shear stress as the mechanical stimuli regulating tissue differentiation and the strain energy as the mechanical stimulus regulating bone resorption. They used an axisymmetric biphasic model of finite elements of a fracture and applied movements on the cortical bone in an attempt to predict typical healing patterns including callus growth. The results were that larger movements increased callus size and delayed bone healing.

The hypothesis introduced by Prendergast et al. [120] was that substrate strain and fluid flow are the primary biophysical stimuli for stem cell differentiation. This hypothesis was proposed based on empirical evidence that differentiated cells respond to biophysical stimuli, e.g. Kaspar et al. [121] placed osteoblasts on a plate subjected to four-point bending and recorded increases in matrix synthesis (collagen Type I) and reductions in synthesis of certain signalling molecules; in a similar experiment Owan et al., [122] found that fluid flow was a dominant stimulus over substrate strain; finally, fluid flow is known to stimulate anabolic cell expressions during in vitro testing [123]. Prendergast et al., [120] used a poroelastic theory to compute the fluid flow and substrate strain in the tissue, and these are used as a basis for the stimulus S for cell differentiation as follows:

 (7) 

where γ is the octahedral shear strain, v is the interstitial fluid flow velocity, a=3.75% and b=3μms^-1 are empirical constants. Simulation of the time-course of tissue differentiation was presented by Huiskes et al., [124] using the stimuli of strain in the solid matrix and fluid flow as proposed in Prendergast et al. [120] (Figure 6).

 Figure 6 

Schematic of the mechano-regulation model proposed by Prendergast et al. [120]. At the beginning there is granulation tissue with mesenchymal stem cells. These are subjected to mechanical stimulation, represented by octahedral shear strain and fluid flow. Some combination of these stimuli will act and change over time. This change is represented on the figure as a change to form fibrous tissue (full line) or a change to form bone (dotted line).

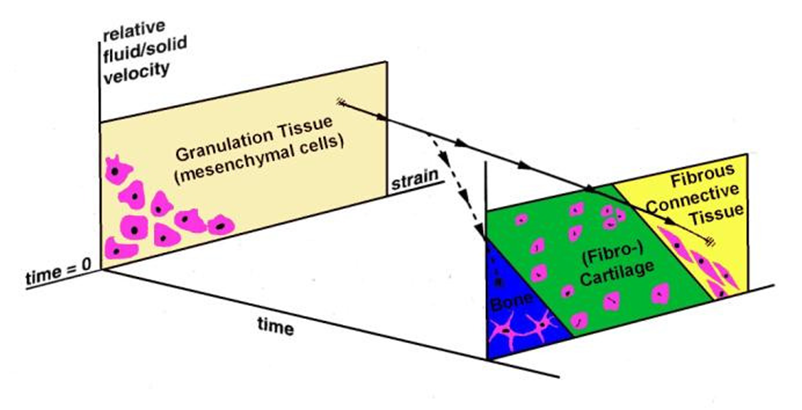
The solid line shows what would occur in an environment where a high shear persists (i.e. maintenance of fibrous tissue and inhibition of ossification) whereas the dashed line shows what would occur if the presence of the soft tissue could progressively reduce the micromotions (i.e ossification would occur).

Isaksson et al. [125] hypothesized that tissue differentiation during normal fracture healing can be equally well regulated by the individual mechanical stimulus represented by the deviatoric strain, pore pressure or fluid velocity. They found that none of the volumetric components, i.e. pore pressure or fluid velocity, alone were able to correctly predict spatial or temporal tissue distribution during fracture healing. However, simulation as a function of only deviatoric strain accurately predicted the course of normal fracture healing. This allowed to conclude that the deviatoric component may be the most significant mechanical parameter to guide tissue differentiation during indirect fracture healing.

Gómez-Benito et al. [126], presented a mathematical model to simulate the effect of mechanical stimuli on most of the cellular processes that occur during fracture healing, namely proliferation, migration and differentiation. On the basis of these three processes, the developed model simulated the evolution of geometry, distributions of cell types and elastic properties inside a healing fracture. The three processes were implemented in a finite element code as a combination of three coupled analysis stages: a biphasic, a diffusion and a thermoelastic step. The process of bone healing was simulated as a process driven by a mechanical stimulus, Ψ(x,t) assumed to be the second invariant of the deviatoric strain tensor (J₂):

 (8) 

where x is the spatial location, t the time, ε_I, ε_II and ε_III the principal strains, and ε_oct=(ε_I+ε_II+ε_III)/3 the octahedral strain.

Isaksson et al. [127], presented and applied to fracture repair a new model of cell and tissue differentiation, using a mechanistic approach. The model directly couples cellular mechanisms to mechanical stimulation during bone healing and is based on the belief that the cells act as transducers during tissue regeneration. In the model, the cells within the matrix proliferate, differentiate, migrate, and produce extracellular matrix, all at cell phenotype specific rates, based on the mechanical stimulation they experience. The model is assembled from coupled partial differentiation equations, which were solved using a newly developed finite element formulation. The evolution of four cell types, i.e. mesenchymal stem cells, fibroblasts, chondrocytes and osteoblasts, and the production of extracellular matrices of fibrous tissue, cartilage and bone were calculated. The material properties of the tissues were iteratively updated based on actual amounts of extracellular matrix in material elements at progressive time points.

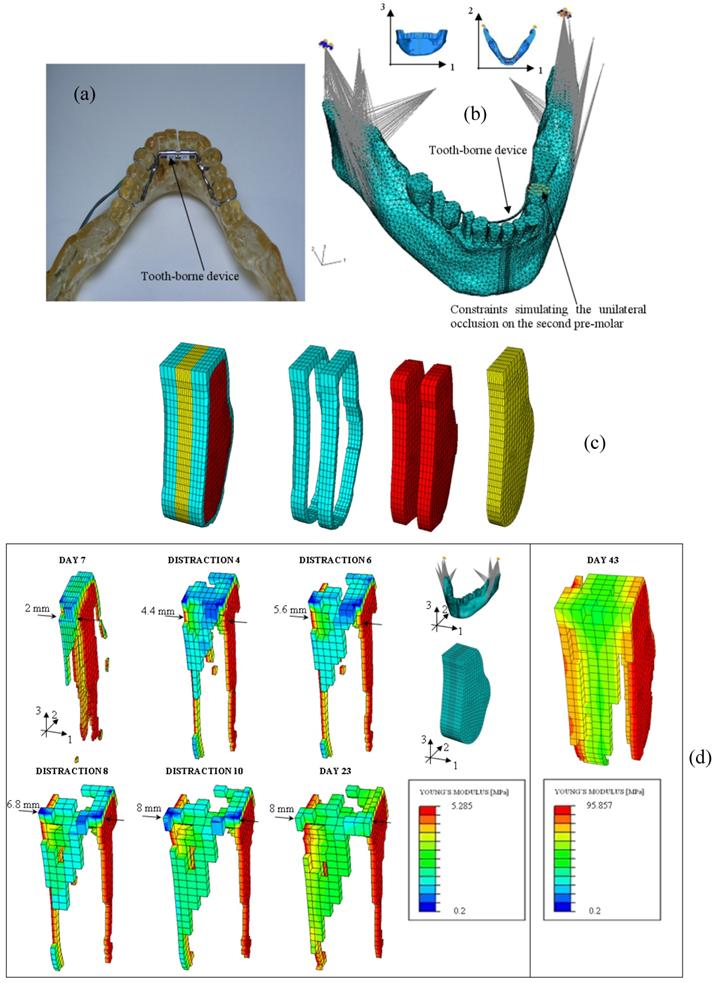
Many clinical applications of these mechano-regulation models can be found in literature: Lacroix and Prendergast [86] predicted the patterns of tissue differentiation during fracture healing of long bones; Andreykiv et al. [88] and Moreo et al. [128, 129] simulated the bone ingrowth on the surface of a glenoid component and of endosseous implants, respectively; Boccaccio et al. determined the optimal rate of expansion [89] (Figure 7) and the optimal duration of the latency period [90, 130] in a mandibular symphyseal distraction osteogenesis; Shefelbine et al. [131] simulated the fracture healing process in cancellous bone; Boccaccio et al. [132], adopting a multi-scale approach predicted the patterns of tissue differentiation observed in a lumbar vertebral fracture.

The algorithms above reviewed are based on theories of mechano-transduction, the way in which cells sense and respond to mechanical forces or displacements. Other bio-regulatory theories have been reported in literature that put in relationship biochemical factors with the spatial and temporal patterns of tissue differentiation observed during the healing process of a fractured bone.

Bailón-Plaza and van der Meulen [92] presented a two-dimensional mathematical model of the bone healing process for moderate fracture gap sizes and fracture stability. The inflammatory and tissue regeneration stages of healing were simulated by modeling mesenchymal cell migration; mesenchymal cell, chondrocyte and osteoblast proliferation and differentiation, and extracellular matrix synthesis and degradation over time. The effects of two generic growth factors on cell differentiation were based on the experimentally studied chondrogenic and osteogenic effects of bone morphogenetic proteins-2 and 4 and transforming growth factor-β-1, respectively. The model successfully simulated the progression of healing and predicted that the rate of osteogenic growth factor production by osteoblasts and the duration of the initial release of growth factors upon injury are particularly important parameters for complete ossification and successful healing.

Geris et al. [133], presented a continuous mathematical model that describes the different fracture healing stages and their response to biochemical stimuli. The model consists of a system of nonlinear partial differential equations describing the spatiotemporal evolution of concentrations and densities of the cell types, extracellular matrix types and growth factors indispensable to the healing process. The model starts after the inflammation phase, when the fracture callus has already been formed. Cell migration was described using not only haptokinetic, but also chemotactic and haptotactic influences. Cell differentiation was controlled by the presence of growth factors and sufficient vascularisation. Matrix synthesis and growth factor production were controlled by the local cell and matrix densities and by the local growth factor concentrations.

Mechanobiology in Bone Tissue Engineering

The design of scaffolds for bone tissue engineering includes a large number of factors related to structural integrity, superficial properties, incubating and cell growth conditions, and cell/biomaterial interactions [134]. One of the main factors that have an influence on the cellular and molecular mechanisms is the biophysical stimulus transmitted to the mesenchymal tissue [135]. This stimulus is linked to the architecture and the material properties of the scaffold that will serve as a host to receive external stimuli for matrix production. The ideal scaffold is capable of transferring the most favourable stimulus on the regenerating tissue hence allowing the times for the regeneration to be reduced and the optimal mechanical properties of the regenerate to be obtained. Mechano-regulation models can be utilized in bone tissue engineering to optimize the morphology, the porosity, the mechanical properties etc of scaffolds as well as the environment conditions. Such an issue has been recently investigated in different studies.

Kelly and Prendergast [97] developed a mechano-regulation algorithm for tissue differentiation to determine the influence of scaffold material properties on chondrogenesis in a finite element model of an osteochondral defect. The model predicted that increasing the stiffness of the scaffold increases the amount of cartilage formation and reduces the amount of fibrous tissue formation in the defect, but this only holds true up to a certain threshold stiffness above which the amount of cartilage formed is reduced.

 Figure 7 

(a) Epoxy resin model - built with Rapid Prototyping techniques - of the mandible with a tooth borne distraction device; (b) FEM model of the mandible with the tooth borne device and boundary and loading conditions adopted. In the model are simulated the temporomandibular joint disc, the unilateral occlusion on the second premolar and the action of the six most important muscles involved during the mastication phase. (c) FEM model of the osteotomized region. Different regions and materials included in the model: cortical bone (in light blue), cancellous bone (in red), fracture callus (in yellow). (d) Patterns of bone tissue which form during the distraction period.

Olivares et al. [136], studied the interactions between scaffold pore morphology, mechanical stimuli developed at the cell microscopic level, and culture conditions applied at the macroscopic scale on two regular scaffold structures. Gyroid and hexagonal scaffolds of 55% and 70% porosity were modeled in a finite element analysis and were submitted to an inlet fluid flow or compressive strain. The authors then, applied the mechano-regulation theory of Prendergast et al. [120] to determine the influence of each structures on the mechanical stimuli on initial conditions. Results indicated that gyroid architectures provide a better accessibility of the fluid than hexagonal structures. Therefore, based on the mechano-regulation theory, the differentiation process in these structures appears more sensitive to inlet fluid flow than axial strain of the scaffold.

Milan et al. [137], developed a computational mechano-regulation model to predict bone tissue formation stimulated mechanically by overall dynamical compression within a porous polymeric scaffold rendered by micro-CT. The model predicted homogeneous mature bone tissue formation under strain levels of 0.5-1% at strain rates of 0.0025-0.005 s^-1. Under higher levels of strain and strain rates, the scaffold showed heterogeneous mechanical behaviour which leads to the formation of a heterogeneous tissue with a mixture of mature bone and fibrous tissue.

The same Authors [138], developed another computational model based on finite element method and computational fluid dynamics to analyse the mechanical stimuli in a composite scaffold made of polylactic acid (PLA) matrix with calcium phosphate glass (Glass) particles. Different bioreactor loading conditions were simulated within the scaffold. Results of the model showed that during perfusion test an inlet velocity of 25 μm/s generates on scaffold surface a fluid flow shear stress which may stimulate osteogenesis.

Byrne et al. [139] (Figure 8) proposed a computational/mechano-biological approach suggesting how best to combine the various design parameters, e.g. scaffold porosity, Young's modulus, and dissolution rate. The numerical simulations predicted that all three design variables have a critical effect on the amount of bone regenerated, but not in an intuitive way: in a low load environment, a higher porosity and higher stiffness but a medium dissolution rate gives the greatest amount of bone whereas in a high load environment the dissolution rate should be lower otherwise the scaffold will collapse—at lower initial porosities however, higher dissolution rates can be sustained.

 Figure 8 

Finite element model of the regular scaffold developed by Byrne et al. [139]. Due to the symmetry of the scaffold only one-eighth of the porous region was modelled. Initially, there are no bone cells but, over time, mesenchymal stem cells proliferate and differentiate and then, the amounts of bone increase. Lower loads, lead to formation of greater amounts of bone tissue. Adapted/Reprinted from [139] Biomaterials, Vol. 28, Issue 36, Byrne DP, Lacroix D, Planell JA, Kelly DJ, Prendergast PJ, Simulation of tissue differentiation in a scaffold as a function of porosity, Young's modulus and dissolution rate: Application of mechanobiological models in tissue engineering, Pages No. 5544-5554, Copyright (2007) with permission from Elsevier.

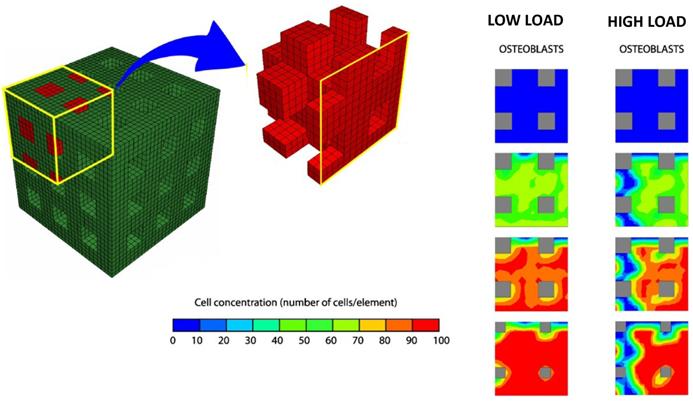
Sanz-Herrera et al. [140] through a multi-scale mechano-regulation model elucidated the effect of scaffold stiffness, porosity, resorption kinetics, pore size and pre-seeding on bone tissue regeneration. The model predicted an increasing rate of bone regeneration with increasing scaffold stiffness, scaffold mean pore size and pre-seeding and the collapse of the scaffold for a faster biomaterial resorption kinetics.

Sandino et al. [141], through a micro computed tomographed (CT)-based finite element (FE) model investigated the effect of the mechanical stimuli and the capillary network formation on cell differentiation within a scaffold of irregular morphology. A porous scaffold of calcium phosphate based glass was simulated and compressive strains of 0.5 and 1% of total deformation were applied. The model revealed that when 0.5% of strain is applied, 70% of the pore volume is affected by mechano-regulatory stimuli corresponding to bone formation; however, because of the lack of oxygen, only 40% of the volume is filled with osteoblasts; when the mechanical strain is increased to 1%, 11% of the pore volume results to be filled with osteoblasts.

An interesting application of mechano-regulation algorithms in Tissue Engineering is the development of models of bioreactors. Bioreactors are mechanical devices that allow control of mechanical stimuli applied on cells or on a scaffold developed for a given tissue engineering application [142]. The bone chamber constitutes a relatively reproducible and mechanically controlled environment that is, in principle, well suited for corroboration of mechanobiological simulations of tissue differentiation. This approach has been adopted by Khayyeri et al. [143] that corroborated the mechano-regulation model of Prendergast and Colleagues [120]. They performed simulations of an in vivo bone chamber experiment and compared numerical results with experimental data. Modelling of bioreactors allows also, to determine the optimal parameters governing the scaffold performances. Khayyeri et al. [144] combined a lattice-based model of a 3D porous scaffold construct derived from micro CT and a mechanobiological simulation of a bone chamber experiment to investigate the effect of scaffold stiffness on tissue differentiation inside the chamber. The results indicate that higher scaffold stiffness, holding pore structure constant, enhances bone formation.

As stated above, mechano-regulation models can be used to optimize the scaffold morphology and, specifically, the shape and the size of the pores, their spatial distribution, the number of pores on a given surface/volume, etc. The scaffold geometry resulting from the optimization process can be very complex and, in general, due to the technological limitations, the traditional manufacturing techniques could not be capable of realizing such objects. The new and emerging fabrication technologies currently utilized to manufacture scaffolds such as rapid prototyping (RP) or solid free form (SFF) permit to overcome these limitations thus allowing to realize every kind of scaffolds with the more disparate geometries. Other advantages that these techniques can offer are the possibility of realizing scaffolds with a customized external shape as well as with structures to increase the mass transport of oxygen and nutrients [145 -147].

Discussion and Conclusions

Bone tissue engineering is an emerging area in bioengineering at the frontiers between biomaterials, biology and biomechanics. Scaffold design for bone tissue engineering applications involves many parameters that directly influence the rate of tissue regeneration onto its microstructural surface. To improve scaffold functionality, increasing interest is being focused on in vitro and in vivo research in order to obtain the optimal scaffold design for a specific application. However, the evaluation of the effect of each specific scaffold parameter on tissue regeneration using these techniques requires costly protocols and long-term experiments. A strategy recently adopted to obtain the optimal scaffold design consists in using mechano-regulation and finite element models that simulate the load transfer from the scaffold microstructure to the regenerate hence allowing the determination of the biophysical stimulus acting onto the cells. By following this approach different mathematical models have been developed and the optimal values for factors such as scaffold stiffness, porosity, resorption kinetics, pore size and pre-seeding, have been found [97, 136-141].

A vital issue for mechano-biological FE models is to what extent they can be simplified without loosing their potential to obtain meaningful results. On the one hand, simplicity is dictated by contemporary computational technology, and on the other it depends on the hypothesis to be tested. One can only make conclusions about phenomena accounted for in the model, not about what is omitted or assumed not to contribute. Different are the limitations of the above reviewed mechano-regulation algorithms. The main criticism raised against the models of Pauwels [110], Carter and colleagues [114, 115] and Claes and Heigele [116] is that there are several reasons that interstitial fluid flow could be a more realistic mechanical variable for feedback information to the cells during tissue differentiation than hydrostatic pressure [122, 123, 148]. The interfragmentary strain theory, although has the advantage of being simple to be used since interfragmentary movement can be easily monitored, presents the limitation that it models the fracture as a one dimensional entity thus ignoring the three dimensional complexity of the callus. Moreover, the theory was mainly conceptualised from primary healing fractures and therefore does not account for the different mechanical environments in the external callus during secondary healing which is a more common process. The model of Prendergast et al. [120] although takes into account the interstitial fluid flow neglects osmotic effects and charged-density flows in the tissue [149].

Several mechano-regulation algorithms proposed to control tissue differentiation during bone healing have been shown to accurately predict temporal and spatial tissue distributions during normal fracture healing. As these algorithms are different in nature and biophysical parameters, it raises the question of which reflects the actual mechanobiological processes the best. Isaksson et al. [150], addressed this issue by corroborating the mechano-regulatory algorithms with more extensive in vivo bone healing data from animal experiments. The authors developed a poroelastic three-dimensional finite element model of an ovine tibia and used this model to simulate the course of tissue differentiation during fracture healing in an adaptive model. The mechanical conditions applied were similar to those used experimentally, with axial compression or torsional rotation as two distinct cases. Histological data at 4 and 8 weeks, and weekly radiographs, were used for comparison. Several mechano-regulation algorithms were investigated: the model proposed by Carter and colleagues [114, 115], that of Claes and Heigele [116], that of Prendergast and coworkers [120] and, finally, the model of Isaksson et al. [125] (algorithm regulated by deviatoric strain alone). In torsion, the algorithms regulated by strain and hydrostatic pressure [114, 115, 116] failed to predict healing and bone formation as seen in experimental data. The algorithm regulated by deviatoric strain and fluid velocity [120] predicted bridging and healing in torsion, as observed in vivo. The predictions of the algorithm regulated by deviatoric strain alone [125] did not agree with in vivo data. None of the algorithms predicted patterns of healing entirely similar to those observed experimentally for both loading modes. However, patterns predicted by the algorithm based on deviatoric strain and fluid velocity was closest to experimental results. It was the only algorithm able to predict healing with torsional loading as seen in vivo. Khayyery et al. [143] further corroborated the Prendergast's model [120] by performing simulations of an in vivo bone chamber and comparing the numerical results with experimental data. The model was implemented to predict tissue differentiation inside mechanically controlled bone chambers inserted into rat tibae. To simulate cell activity, a lattice approach with stochastic cell migration, proliferation, and selected differentiation was adopted; because of its stochastic nature, each run of the simulation gave a somewhat different result. Simulations predicted the load-dependency of the tissue differentiation inside the chamber and a qualitative agreement with histological data; however, the full variability found between specimens in the experiment could not be predicted by the mechano-regulation algorithm. Such a result raised the question whether tissue differentiation predictions can be linked to genetic variability in animal populations.

Another important issue for computational mechanobiology is represented by the fact that the mechano-regulatory algorithms include empirical constants, whose values must be determined by comparison to a biological reality. The osteogenic ossification rule [114, 115], for example, contains the constant k (see equation (6)), which weights the sensitivity of the tissue for hydrostatic stress relative to shear stress in the index I. In the mechano-regulation rule developed by Prendergast et al. [120] the constants b and a [124] (see equation (7)) weight the relative sensitivities for fluid flow velocity and octahedral shear strain, respectively. These constants do not have a specific physical meaning and can be determined by following the 'trial and error' method outlined in van der Melulen and Huiskes [3]: “Computational mechano-biologists hypothesize a potential rule and determine if the outcome of this hypothesis produces realistic tissue structures and morphologies, hence 'trial-and-error'. If the results correspond well, they might be an explanation for the mechanism being modelled. This method of research is common practice and productive in physics, less common in biology [151]; although 'theoretical biology' is based on this type of approach”. Certainly, physicists use this approach (the computational gedanken experiment) because there are so few rules in Physics and the predictions are amenable to exact quantitative testing. In Biology the phenomena to be observed and analysed are much more complicated than in Physics, so cut-and-try theoretical experimentation could not be really useful. At this point it is legitimate to raise the question: is this philosophy of biological research correct? Further research should be carried out on the topic.

In the cases when a direct experimental observation of tissue regeneration processes is not affordable, mechanobiology becomes an absolutely necessary tool. For example, the histological analyses, due to their intrusive nature, cannot be utilized to quantify the amounts of human tissues forming during regeneration processes at different time points. In such cases mechanobiology can predict the possible patterns of tissue differentiation and can determine how the mechanical properties of the differentiating tissues change in time. The mechanobiologists, calibrate their mechano-regulation model through experimental data obtained by animal models (or experimental data measured in clinical cases similar to that studied) and extrapolate the results of the model to the specific clinical application under analysis.

One of the most interesting results reported by Byrne et al. [139] is that the tissue differentiation process occurring within a scaffold is significantly depending on the magnitude of the load acting on it. In a low loading environment, high porosities and higher stiffness but a medium dissolution rate gives the greatest amount of bone. Alternatively the initial porosity and rate of dissolution should be lower in a high loading environment in order to maintain the mechanical and structural integrity of the bone-scaffold system. Such a finding indicates that the boundary and loading conditions utilized in a mechano-regulation model simulating the interaction between the scaffold and the anatomic site where it is implanted must be modelled very carefully and must be patient specific. A possible strategy that mechanobiologists can adopt to solve the problem of accurately simulating the boundary and loading conditions acting on bone scaffolds consists in using the multi-scale approach. Two models have to be built: a macro-scale model simulating the anatomical site where the scaffold will be implanted and a micro-scale model simulating the scaffold and the tissues surrounding it. Localization rules can be used to determine, from the macro-scale model, the boundary and loading conditions acting on the micro-scale model. Homogenization rules can be used to determine, from the micro-scale model, the equivalent mechanical properties to implement in the macro-scale model. Recently the multi-scale approach has been applied to tissue engineering for bone regeneration [140]. Such approaches will be translated into the clinical side with the development of patient-specific multi-scale studies [152].

Future perspectives include the development of computer power. This should inevitably lead to more complex models of higher size being studied. A more robust integration is required, in future, between biology, mechanics and materials science. This should lead to the development of mechano-regulation models that more accurately describe physiological processes such as the fracture healing, the tissue genesis etc. Future perspectives of numerical simulations of biomaterial scaffolds for bone tissue engineering rely also on the development of new methods to account for the multi-scale dimension of the problems.

As a conclusion, bone tissue engineering is an emerging multidisciplinary field that can revolutionize the ways we improve the health and quality of life for millions of people worldwide. The future of computational models integrating the finite element method and mechano-regulation algorithms appears promising. More realistic models of biological/physiological processes need to be simulated; however, in order to make the implementation of these algorithms, affordable for a clinical use, more efforts need to be put into the development of powerful computational tools.

Conflict of Interests

The authors have declared that no conflict of interest exists.

References

1. Bianco P, Robey PG. Stem cells in tissue engineering. Nature. 2001;414:118-21

2. Langer R, Vacanti J P. Tissue engineering. Science. 1993;260:920-6

3. van der Meulen MCH, Huiskes R. Why mechanobiology? A survey article. J Biomech. 2002;35:401-14

4. Bölgen N, Yang Y, Korkusuz P. et al. Three-Dimensional Ingrowth of Bone Cells Within Biodegradable. Tissue Eng Part A. 2008;14:1743-50

5. Duty AO, Oest ME, Guldberg RE. Cyclic Mechanical Compression Increases Mineralization of Cell-Seeded Polymer Scaffolds In Vivo. J Biomech Eng. 2007;129:531-9

6. Hung CT, Mauck RL. et al. A Paradigm for Functional Tissue Engineering of Articular Cartilage via Applied Physiologic Deformational Loading. Ann Biomed Eng. 2004;32:35-49

7. Kisiday JD, Jin M, Dimicco MA. et al. Effects of dynamic compressive loading on chondrocyte biosynthesis in self-assembling peptide scaffolds. J Biomech. 2004;37:595-604

8. Waldman SD, Couto DC, Grynpas MD. A single application of cyclic loading can accelerate matrix deposition and enhance the properties of tissue-engineered cartilage. Osteoarthr Cartil. 2006;14:323-330

9. Karageorgiou V, Kaplan D. Porosity of 3D biomaterial scaffolds and osteogenesis. Biomaterials. 2005;26(27):5474-91

10. Zienkiewicz OC, Taylor RL. The finite element method, vol. 1 and 2. New York: McGraw-Hill. 1991

11. Huiskes R, Chao EYS. A survey of finite element analysis in orthopedic biomechanics: the first decade. J Biomech. 1983;16(6):385-409

12. Prendergast PJ. Finite element models in tissue mechanics and orthopaedic implant design. Clin Biomech. 1997;12(6):343-66

13. Hollister SJ, Brennan JM, Kikuchi N. A homogenization sampling procedure for calculating trabecular bone effective stiffness and tissue level stress. J Biomech. 1994;27:433-44

14. Müller R, Hildebrand T, Rüegsegger P. Non invasive bone biopsy: a new method to analyse and display the three dimensional structure of trabecular bone. Phys Med Biol. 1994;39:145-64

15. Lengsfeld M, Schmitt J, Kaminsky AP. et al. Comparison of geometry-based and CT voxel-based finite element modelling and experimental validation. Med Eng Phys. 1998;20:515-22

16. Holzapfel GA, Stadler M, Schulze-Bauer CAJ. A layer-specific three-dimensional model for the simulation of balloon angioplasty using magnetic resonance imaging and mechanical testing. Ann Biomed Eng. 2002;30:753-67

17. Boccaccio A, Lamberti L, Pappalettere C. et al. Accuracy of finite element predictions on bone/implant interface contact pressures for models reconstructed from CT scans. J Mech Med Biol. 2008;8(2):161-82

18. Schim VB, Pitto RP, Streicher RM. et al. The use of sparse CT datasets for auto-generating accurate FE models of the femur and pelvis. J Biomech. 2007;40:26-35

19. Gao J, Ding Z. 3D finite element mesh generation of complicated tooth model based on CT slices. Comput Methods Programs Biomed. 2006;82:97-105

20. Boccaccio A, Lamberti L, Pappalettere C. et al. Mechanical behavior of an osteotomized mandible with distraction orthodontic devices. J Biomech. 2006;39:2907-18

21. Boccaccio A, Lamberti L, Pappalettere C. et al. Comparison of different distraction orthodontic devices: a finite element study. Am J Orthod Dentofacial Orthop. 2008;134(2):260-69

22. Boccaccio A, Cozzani M, Pappalettere C. Analysis of the performance of different orthodontic devices for mandibular symphyseal distraction osteogenesis. Eur J Orthod. 2010 in press

23. Keyak JH, Rossi SA, Jones KA. et al. Prediction of femoral fracture load using automated finite element modelling. J Biomech. 1998;31:125-33

24. Guldberg RE, Hollister SJ, Charras GT. The accuracy of image-based finite element models. Transactions of the ASME, J Biomech Eng. 1998;120:289-95

25. Tanck E, Homminga J, Van Lenthe GH. et al. Increase in bone volume fraction precedes architectural adaptation in growing bone. Bone. 2001;28:650-4

26. Van Rietbergen B, Huiskes R, Eckstein F. et al. Trabecular bone tissue strains in the healthy and osteoporotic human femur. J Bone Miner Res. 2003;18:1781-8

27. Homminga J, Van Rietbergen B, Lochmüller EM. et al. The osteoporotic vertebral structure is well adapted to the loads of daily life, but not to infrequent “error” loads. Bone. 2004;34:510-6

28. Crawford RP, Cann CE, Keaveny TM. Finite element model predict in vitro vertebral body compressive strength better than quantitative computed tomography. Bone. 2003;33:744-50

29. Natali AN, Viola MM. Computer tomography for virtual models in dental imaging. Natali, Viola eds. London: Taylor & Francis. 2003:34-51

30. Grosland NM, Brown TD. A voxel-based formulation for contact finite element analysis. Comp Meth Biomech Biomed Eng. 2002;5:21-32

31. Boyd SK, Müller R. Smooth surface meshing for automated finite element model generation from 3D image data. J Biomech. 2007;39:1287-95

32. Charras GT, Guldberg RE. Improving the local solution accuracy of large-scale digital image-based finite element analyses. J Biomech. 2000;33:255-59

33. Boccaccio A, Lamberti L, Pappalettere C. et al. Evaluation and minimization of reconstruction errors in FEM models generated from CT-scan images. J Mech Med Biol. 2008;9:301-27

34. Feldkamp LA, Goldstein SA, Parfitt AM. et al. The direct examination of 3-dimensional bone architecture in vitro by computed tomography. J Bone Miner Res. 1989;4:3-11

35. De Santis R, Anderson P, Tanner KE. et al. Bone fracture analysis on the short rod chevron-notch specimens using the X-ray computer micro-tomography. J Mater Sci Mater Med. 2000;10:629-36

36. Lacroix D, Planell JA, Prendergast PJ. Computer-aided design and finite element modelling of biomaterial scaffolds for bone tissue engineering. Phil Trans R Soc A. 2009;367:1993-2009

37. van Lenthe GH, Hagenmüller H, Bohner M. et al. Nondestructive micro-computed tomography for biological imaging and quantification of scaffold-bone interaction in vivo. Biomaterials. 2007;28:2479-90

38. Porter BD, Lin AS, Peister A. et al. Noninvasive image analysis of 3D construct mineralization in a perfusion bioreactor. Biomaterials. 2007;28:2525-33

39. Komlev VS, Peyrin F, Mastrogiacomo M. et al. Kinetics of in vivo bone deposition by bone marrow stromal cells into porous calcium phosphate scaffolds: an X-ray computed microtomography study. Tissue Eng. 2006;12:3449-58

40. Lacroix D, Chateau A, Ginebra MP. et al. Micro-finite element models of bone tissue-engineering scaffolds. Biomaterials. 2006;27:5326-34

41. Sandino C, Planell JA, Lacroix D. A finite element study of mechanical stimuli in scaffolds for bone tissue engineering. J Biomech. 2008;41:1005-14

42. Boccaccio A, Vena P, Gastaldi D. et al. Finite element analysis of cancellous bone failure in the vertebral body of healthy and osteoporotic subjects. Proc Inst Mech Eng H. 2008;222(7):1023-36

43. Caplan AI. The mesengenic process. Clin Plast Surg. 1994;21:429-35

44. Prendergast PJ. Computational Mechanobiology. In: (ed.) Cerrolaza M, Doblaré M, Martinez G, Calvo B. Compuational Bioengineering: current trends and applications. London: Imperial College Press. 2004:117-33

45. Jones WR, Ting-beall HP, Lee GM. et al. Alterations in the Young's modulus and volumetric properties of chondrocytes isolated from normal and osteoarthritic human cartilage. J Biomech. 1999;32:119-27

46. Charras GT, Horton MA. Single cell mechanotransduction and its modulation analyzed by atomic force microscopy indentation. Biophys J. 2002;82:2970-81

47. Prendergast PJ. Computational modelling of cell and tissue mechanoresponsiveness. Gravitational and Space Biology. 2007;20:43-50

48. Kelly DJ, Jacobs CR. The Role of Mechanical Signals in Regulating Chondrogenesis and Osteogenesis of Mesenchymal Stem Cells. Birth Defects Res C Embryo Today. 2010;90:75-85

49. Einhorn TA. The cell and molecular biology of fracture healing. Clin Orthop Relat Res. 1998;355:S7-S21

50. McKibbin B. The biology of fracture healing in long bones. J Bone Joint Surg. 1978;60:150-62

51. Iwaki A, Jingushi S, Oda Y. et al. Localization and quantification of proliferating cells during rat fracture repair: detection of proliferating cell nuclear antigen by immunochemistry. J Bone Miner Res. 1997;12:96-102

52. Sandberg MM, Aro HT, Vuorio EI. Gene expression during bone repair. Clin Orthop Relat Res. 1993;289:292-312

53. Doblaré M, García JM, Gómez MJ. Modelling bone tissue fracture and healing: a review. Eng Fract Mech. 2004;71:1809-40

54. Huiskes R. Failed innovation in total hip-replacement - diagnosis and proposals for a cure. Acta Orthop Scand. 1993;574:699-716

55. Prendergast PJ. Prosthesis fixation for orthopaedics. In: (ed.) Webster JE. Encyclopaedia of Medical Devices and Instrumentation. New Jersey: Wiley. 2006:192-8

56. Martin I, Wendt D, Heberer M. The role of bioreactors in tissue engineering. Trends Biotechnol. 2004;22:80-6

57. Prendergast PJ, Checa S, Lacroix D. Computational Models of Tissue Differentiation. In: (ed.) De S. et al. Computational modelling in Biomechanics. NY: Springer Science. 2009:353-72

58. Schwarz US, Bischofs IB. Physical determinants of cell organization in soft media. Med Eng Phys. 2005;27:763-72

59. Lo C-M, Wang H-B, Dembo M, Wang Y-L. Cell movement is guided by the rigidity of the substrate. Biophys J. 2000;79:144-52

60. Wong JY, Velasco A, Rajagopalan P. et al. Directed movement of vascular smooth muscle cells on gradient-compliant hydrogels. Langmuir. 2003;19:1908-13

61. Bischofs IB, Schwarz US. Cell organization in soft media due to active mechanosensing. Proc Natl Acad Sci USA. 2003;100:9274-9

62. Dalby MJ, Riehle MO, Sutherland DS. et al. Fibroblast response to a controlled nanoenvironment produced by colloidal lithography. J Biomed Mater Res. 2004;69:314-22

63. Dunn GA, Heath JP. New hypothesis of contact guidance in tissue cells. Exp Cell Res. 1976;101:1-14

64. Sanz-Herrera JA, Moreo P, García-Aznar JM. et al. On the effect of substrate curvature on cell mechanics. Biomaterials. 2009;30:6674-86

65. Carter SB. Haptotaxis and mechanism of cell motility. Nature. 1967;213:256-60

66. Bray D. Cell movements: from molecules to motility; 2nd ed. New York: Garland. 2001

67. Merryman WD, Engler AJ. Innovations in cell mechanobiology. J Biomech. 2010;43:1

68. Dahl KN, Booth-Gauthier EA, Ladoux B. In the middle of it all: mutual mechanical regulation between the nucleus and the cytoskeleton. J Biomech. 2010;43:2-8

69. Stricker J, Falzone T, Gardel ML. Mechanics of the F-actin cytoskeleton. J Biomech. 2010;43:9-14

70. Qin Z, Buehler MJ, Kreplak L. A multi-scale approach to understand the mechanobiology of intermediate filaments. J Biomech. 2010;43:15-22

71. Hawkins T, Mirigian M, Yasar MS. et al. Mechanics of microtubules. J Biomech. 2010;43:23-30

72. Constantinou PE, Diehl MR. The mechanochemistry of integrated motor protein complexes. J Biomech. 2010;43:31-7

73. Chen FH, Song L, Mauck RL. et al. Mesenchymal stem cells. Lanza R et al, eds. Principles of Tissue Engineering, 3rd ed US: Academic Press: 2007: 823-843

74. Owen M. The origin of bone cells in the postnatal organism. Arthritis Rheum. 1980;23:1073-9

75. Simmons DJ. Fracture healing perspectives. Clin Orthop Rel Res. 1985;200:100-113

76. Brighton CT, Hunt RM. Early histological and ultrastructural changes in medullary fracture callus. J Bone Joint Surg. 1991;73:832-47

77. Glowacki J. Angiogenesis in fracture repair. Clin Orthop Rel Res. 1998;355:S82-S89

78. Yoo JU, Johnstone B. The role of osteochondral progenitor cells in fracture repair. Clin Orthop Rel Res. 1998;355:S73-S81

79. Barry FP, Murphy JM. Mesenchymal stem cells: clinical applications and biological characterization. Int J Biochem Cell Biol. 2004;36:568-84

80. Ballini A, De Frenza G, Cantore S. et al. In vitro stem cell cultures from human dental pulp and periodontal ligament: new prospects in dentistry. Int J Immunopathol Pharmacol. 2007;20:9-16

81. Ballini A, Capodiferro S, Cantore S. et al. Dental pulp stem cells curriculum vitae. Journal of osteology and biomaterials. 2010;1:23-27

82. Mori G, Centonze M, Brunetti G. et al. Osteogenic properties of human dental pulp stem cells. J Biol Regul Homeost Agents. 2010;24:167-75

83. Kearney EM. Influence of tensile strain on rat mesenchymal stem cell proliferation, differentiation and apoptosis (PhD Thesis). Dublin: Trinity College. 2008

84. Byrne DP. Computational modelling of bone regeneration using a three dimensional lattice approach(PhD Thesis). Dublin: Trinity College. 2008

85. Murray JD. Mathematical Biology. Springer-Verlag. 1989

86. Lacroix D, Prendergast PJ. A mechano-regulation model for tissue differentiation during fracture healing: analysis of gap size and loading. J Biomech. 2002;35:1163-71

87. Geris L, Andreykiv A, Oosterwyck HV. et al. Numerical simulation of tissue differentiation around loaded titanium implants in a bone chamber. J Biomech. 2004;37:763-9

88. Andreykiv A, Prendergast PJ, van Keulen F. et al. Bone ingrowth simulation for a concept glenoid component design. J Biomech. 2005;38:1023-33

89. Boccaccio A, Pappalettere C, Kelly DJ. The influence of expansion rates on mandibular distraction osteogenesis: a computational analysis. Ann Biomed Eng. 2007;35(11):1940-60

90. Boccaccio A, Prendergast PJ, Pappalettere C. et al. Tissue differentiation and bone regeneration in an osteotomized mandible: a computational analysis of the latency period. Med Biol Eng Comput. 2008;46(3):283-98

91. Gruler H, Bultmann BD. Analysis of cell movement. Blood cells. 1984;10:61-77

92. Bailón-Plaza A, van der Meulen MCH. A mathematical framework to study the effects of growth factor influences on fracture healing. J Theor Biol. 2001;212:191-209

93. Kelly DJ. Mechanobiology of tissue differentiation during osteochondral defect repair (PhD Thesis). Dublin: Trinity College. 2003

94. Lacroix D, Prendergast PJ, Li G, Marsh D. Biomechanical model to simulate tissue differentiation and bone regeneration: application to fracture healing. Med Biol Eng Comp. 2002;40:14-21

95. Sherratt JA, Martin E, Murrayjd JD. et al. Mathematical models of would healing in embryonic and adult epidermis. IMA J Math Appl Med Biol. 1992;9:177-96

96. Kelly DJ, Prendergast PJ. Mechano-regulation of stem cell differentiation and tissue regeneration in osteochondral defects. J Biomech. 2005;38:1413-22

97. Kelly DJ, Prendergast PJ. Prediction of the optimal mechanical properties for a scaffold used in osteochondral defect repair. Tissue Eng. 2006;12(9):2509-19

98. Jones DB, Nolte H, Scholübbers JG. et al. Biochemical signal transduction of mechanical strain in osteoblast-like cells. Biomaterials. 1991;12:101-10

99. Brighton CT, Strafford B, Gross SB. et al. The proliferative and synthetic response of isolated calvarial bone cells of rats to cyclic biaxial mechanical strain. J Bone Joint Surg. 1991;73:320-31

100. Fermor B, Gundle R, Evans M. et al. Primary human osteoblast proliferation and prostaglandin E₂ release in response to mechanical strain in vitro. Bone. 1998;22:637-43

101. Kasper D, Seidl W, Neidlinger-Wilke C. et al. Proliferation of human-derived osteoblast-like cells depends on the cycle number and frequency of uni-axial strain. J Biomech. 2002;35:873-80

102. Benya PD, Brown PD. Modulation of chondrocyte phenotype in vitro. In: (ed.) Kuettner KE. et al. Articular Cartilage Biochemistry. New York: Raven Press. 1986:219-33

103. Lee DA, Noguchi T, Knight MM. et al. Response of chondrocyte subpopulations cultured within loaded and unloaded agarose. J Orthop Res. 1998;16:726-33

104. Loening AM, James IE, Levenston ME. Injurious Mechanical Compression of Bovine Articular Cartilage Induces Chondrocyte Apoptosis. Arch Biochem Biophys. 2000;381:205-12

105. Quinn TM, Allen RG, Schalet BJ. et al. Matrix and cell injury due to sub-impact loading of adult bovine articular cartilage explants: effects of strain rate and peak stress. J Orthop Res. 2001;19:242-9

106. Kurz B, Jin M, Patwari P. et al. Biosynthetic response and mechanical properties of articular cartilage after injurious compression. J Orthop Res. 2001;19:1140-6

107. Richardson JB, Kenwright J, Cunningham JL. Fracture stiffness measurement in the assessment and management of tibial fractures. Clin Biomech. 1992;7:75-9

108. Pérez MA, Prendergast PJ. Random-walk models of cell dispersal included in mechanobiological simulations of tissue differentiation. J Biomech. 2007;40:2244-53

109. Checa S, Prendergast PJ. A mechanobiological model for tissue differentiation that includes angiogenesis: A lattice-based modeling approach. Ann Biomed Eng. 2009;37:129-45

110. Pauwels F. Eine neue theorie über den einfluβ mechanischer reize auf die differenzierung der stützgewebe. Z Anat Entwickl. Gesch. 1960; 121, 478-515. Translated as A new theory concerning the influence of mechanical stimuli on the differentiation of the supporting tissues. In: (ed.) Maquet P, Furlong R. Biomechanics of the Locomotor apparatus. Berlin: Springer. 1980:375-407

111. Weinans H, Prendergast PJ. Tissue adaptation as a dynamical process far from equilibrium. Bone. 1996;19:143-9

112. Perren SM. Physical and biological aspects of fracture healing with special reference to internal fixation. Clin Orthop Rel Res. 1979;138:175-96

113. Perren SM, Cordey J. The concept of interfragmentary strain. Current concepts of internal fixation of fractures. Berlin: Springer-Verlarg. 1980:63-77

114. Carter DR, Wong M. The role of mechanical loading histories in the development of diarthrodial Joints. J Orthop Res. 1988;6:804-16

115. Carter DR, Blenman PR, Beaupré GS. Correlations between mechanical stress history and tissue differentiation in initial fracture healing. J Orthop Res. 1988;6:736-48

116. Claes LE, Heigele CA. Magnitudes of local stress and strain along bony surfaces predict the course and type of fracture healing. J Biomech. 1999;32:255-66

117. Kuiper JH, Richardson JB, Ashton BA. Mechanical signals in early fracture callus. Vander Sloten J, Lowet G, Van Audekercke R, Van der Perre G, eds. Proc 10th Europ Soc Biomech. 1996:154

118. Kuiper JH, Ashton BA, Richardson JB. Computer simulation of fracture callus formation and stiffness restoration. Prendergast PJ, Lee TC, Carr AJ, eds. Proc 12th Europ Soc Biomech. 2000:61

119. Kuiper JH, Richardson JB, Ashton BA. Computer simulation to study the effect of fracture site movement on tissue formation and fracture stiffness restoration. European Congress on Computational Methods in Applied Sciences and Engineering ECCOMAS. 2000

120. Prendergast PJ, Huiskes R, Søballe K. Biophysical stimuli on cells during tissue differentiation at implant interfaces. J Biomech. 1997;30:539-48

121. Kaspar D, Seidl W, Neidlinger-Wilke C. et al. Dynamic cell stretching increases human osteoblast proliferation and CICP synthesis but decreases osteocalcin synthesis and alkaline phosphatase activity. J Biomech. 2000;33:45-51

122. Owan I, Burr DB, Turner CH. et al. Mechanotransduction in bone: osteoblasts are more sensitive to fluid forces than mechanical strain. Am J Appl Physiol. 1997;273:C810-815

123. Jacobs CR, Yellowley CE, Davis BR. et al. Differential effect of steady versus oscillating flow on bone cells. J Biomech. 1998;31:969-76

124. Huiskes R, van Driel WD, Prendergast PJ. et al. A biomechanical model for periprosthetic fibrous-tissue differentiation. J Mater Sci Mater Med. 1997;8:785- 88

125. Isaksson H, Wilson W, van Donkellaar CC. et al. Comparison of biophysical stimuli for mechano-regulation of tissue differentiation during fracture healing. J Biomech. 2006;39:1507-16

126. Gòmez-Benito MJ, Garcìa-Aznar JM, Kuiper JH. et al. Influence of fracture gap size on the pattern of long bone healing: a computational study. J Theor Biol. 2005;235:105-9

127. Isaksson H, van Donkelaar CC, Huiskes R. A mechano-regulatory bone-healing model incorporating cell-phenotype specific activity. J Theor Biol. 2008;252:230-46

128. Moreo P, Garcìa-Aznar JM, Doblaré M. Bone ingrowth on the surface of endosseous implants: Part 1: Mathematical model. J Theor Biol. 2009;260(1):1-12

129. Moreo P, Garcìa-Aznar JM, Doblaré M. Bone ingrowth on the surface of endosseous implants: Part 2: Theoretical and numerical analysis. J Theor Biol. 2009;260(1):13-26

130. Boccaccio A, Lamberti L, Pappalettere C. Effects of ageing on the latency period in mandibular distraction osteogenesis: a computational mechano-biological analysis. J Mech Med Biol. 2008;8(2):203-25

131. Shefelbine SJ, Augat P, Claes L. et al. Trabecular bone fracture healing simulation with finite element analysis and fuzzy logic. J Biomech. 2005;38:2440-50

132. Boccaccio A, Kelly DJ, Pappalettere C. A Mechano-Regulation Model of Fracture Repair in Vertebral Bodies. J Orthop Res. 2010 In Press

133. Geris L, Gerisch A, Vander Sloten J. et al. Angiogenesis in bone fracture healing: A bioregulatory model. J Theor Biol. 2008;251:137-58

134. Karande TS, Ong JL, Agrawal CM. Diffusion in musculoskeletal tissue engineering scaffolds: design issues related to porosity, permeability, architecture, and nutrient mixing. Ann Biomed Eng. 2004;32:1728-43

135. Schriefer JL, Warden SJ, Saxon LK. et al. Cellular accommodation and the response of bone to mechanical loading. J Biomech. 2005;38:1838-45

136. Olivares A, Marsal E, Planell JA. et al. Finite element study of scaffold architecture design and culture conditions for tissue engineering. Biomaterials. 2009;30:6142-9

137. Milan JL, Planell JA, Lacroix D. Simulation of bone tissue formation within a porous scaffold under dynamic compression. Biomech Model Mechanobiol. 2010 [Epub ahead of print]

138. Milan JL, Planell JA, Lacroix D. Computational modelling of the mechanical environment of osteogenesis within a polylactic acid-calcium phosphate glass scaffold. Biomaterials. 2009;30:4219-26

139. Byrne DP, Lacroix D, Planell JA, Kelly DJ, Prendergast PJ. Simulation of tissue differentiation in a scaffold as a function of porosity, Young's modulus and dissolution rate: application of mechanobiological models in tissue engineering. Biomaterials. 2007;28:5544-54

140. Sanz-Herrera JA, García-Aznar JM, Doblaré M. On scaffold designing for bone regeneration: A computational multiscale approach. Acta Biomater. 2009;5:219-29

141. Sandino C, Checa S, Prendergast PJ. et al. Simulation of angiogenesis and cell differentiation in a CaP scaffold subjected to compressive strains using a lattice modeling approach. Biomaterials. 2010;31:2446-52

142. Martin I, Wendt D, Heberer M. The role of bioreactors in tissue engineering. Trends Biotechnol. 2004;22:80-6

143. Khayyeri H, Checa S, Tägil M. et al. Corroboration of mechanobiological simulations of tissue differentiation in an in vivo bone chamber using a lattice-modeling approach. J Orthop Res. 2009;27:1659-66

144. Khayyeri H, Checa S, Tägil M. et al. Tissue differentiation in an in vivo bioreactor: in silico investigations of scaffold stiffness. J Mater Sci Mater Med. 2010;21:2331-6

145. Cheah CM, Chua CK, Leong KF. et al. Development of a tissue engineering scaffold structure library for rapid prototyping. Part 2: parametric library and assembly program. Int J Adv Manuf Technol. 2003;21(4):302-12

146. Sachlos E, Czernuszka JT. Making tissue engineering scaffolds work. Review: the application of solid freeform fabrication technology to the production of tissue engineering scaffolds. Eur Cells Mater J. 2003;5:29-40

147. Liebschner MAK, Wettergreen MA. Optimization of bone scaffold engineering for load bearing applications. Ashammakhi N, Ferretti P, eds. Topics in Tissue Engineering 2003 1-39

148. Klein-Nulend J, Semeins CM, Burger EH. et al. Response of isolated osteocytes to mechanical loading. In: (ed.) Odgaard A, Weinans H. Bone structure and remodeling. River Edge, London: World Scientific Publishing. 1996:37-49

149. Mow VC, Wang CC-B, Hung CT. The extracellular matrix, interstitial fluid and ions as a mechanical signal transducer in articular cartilage. Osteoarthr Cartil. 1999;7:41-58

150. Isaksson H, Donkellar CC, Huiskes R. et al. Corroboration of mechanoregulatory algorithms for tissue differentiation during fracture healing: Comparison with in vivo results. J Orthop Res. 2006;24:898-907

151. Huiskes R. The law of adaptive bone remodeling: a case for crying newton? In: (ed.) Odgaard A, Weinans H. Bone Structure and Remodeling. River Edge, London, World Scientific Publishing, Singapore. 1995:15-24

152. Kerckhoffs RC, Narayan SM, Omens JH. et al. Computational modeling for bedside application. Heart Fail Clin. 2008;4:371-78

Author contact

Corresponding author: Dr. Antonio Boccaccio, Dipartimento di Ingegneria Meccanica e Gestionale, Politecnico di Bari, Viale Japigia, 182, 70126, Bari, Italy. Tel: +39-080-5962829; Fax: +39-080-5962777; Email: a.boccaccioit. Dr. Andrea Ballini, Department of Dental Sciences and Surgery, University of Bari “Aldo Moro”, Piazza Giulio,Cesare, 11, 70124, Bari, Italy. Tel: +39-080-5594242; Fax: +39 080 5478043; Email: andrea.balliniuniba.it

Received 2010-5-19
Accepted 2010-10-16
Published 2011-1-26

Citation styles

©2024 Ivyspring International Publisher. Terms of use