10
Impact Factor
ISSN: 1449-2288
Int J Biol Sci 2019; 15(6):1148-1160. doi:10.7150/ijbs.33400 This issue Cite
Research Paper
Causal Cortical Network for Arithmetic Problem-Solving Represents Brain's Planning Rather than Reasoning
Faculty of Health Sciences, University of Macau, Macau SAR, China
*These authors contributed equally to this work
Received 2019-1-22; Accepted 2019-4-4; Published 2019-5-7
Abstract
Arithmetic problem-solving whose components mainly involve the calculation, planning and reasoning, is an important mathematical skill. To date, the neural mechanism underlying arithmetic problem-solving remains unclear. In this study, a scheme that combined a novel 24 points game paradigm, conditional Granger causality analysis, and near-infrared spectroscopy (fNIRS) neuroimaging technique was developed to examine the differences in brain activation and effective connectivity between the calculation, planning, and reasoning. We discovered that the performance of planning was correlated with the activation in frontal cortex, whereas the performance of reasoning showed the relationship with the activation in parietal cortex. In addition, we also discovered that the directional effective connectivity between the anterior frontal and posterior parietal cortex was more closely related to planning rather than reasoning. It is expected that this work will pave a new avenue for an improved understanding of the neural underpinnings underlying arithmetic problem-solving, which also provides a novel indicator to evaluate the efficacy of mathematical education.
Keywords: arithmetic problem-solving, planning, reasoning, Granger causality, fNIRS, brain networks
Introduction
Our human beings differ from most other animals in arithmetic problem-solving that is distinct from the calculation. Calculation involves the retrieval of arithmetic facts or the operation of digits, whereas arithmetic problem-solving denotes the goal-directed arithmetic activities that mediate between the existing and desired situations (1,2). Meanwhile, the calculation plays an essential role in the cognitive processing of arithmetic problem-solving, which also strongly depends on the number processing.
To date, although the neural substrates of calculation have been well documented (3), the neural mechanism underlying arithmetic problem-solving remains unclear (4). For example, previous studies have demonstrated that three parietal regions are involved in calculation (3), in which the horizontal segment of intraparietal sulcus (IPS) is associated with the semantic representation of numbers as quantities, the posterior superior parietal lobule (PSPL) is responsible for the spatial representation of numerical quantities, and the left angular gyrus (AG) is essential for the retrieval of mathematical facts. Recent work also revealed that the resting-state functional connectivity (FC) between the ventrotemporal occipital cortex, posterior parietal cortex and prefrontal cortex (PFC) can predict the children's development in calculation (5) while the calculation practice can alter the FC between the frontal and parietal cortex (6). By contrast, only a few studies were performed to inspect the brain activation and networks associated with arithmetic problem-solving (4), in which two paradigms were usually used: 1) the word problem-solving task which can explore the problem representation (1,7), 2) the number series completion task which is able to access the numerical inductive reasoning (8,9). Interestingly, it was discovered that the word problem-solving strongly depends on the semantical ability (1,7), whereas the number series completion is more directly related to number processing (8,9). In addition, previous reports also highlighted that the activation in dorsolateral prefrontal cortex (DLPFC) and IPS was correlated with numerical inductive reasoning (10) while more complex numerical inductive reasoning exhibited enhanced activation in the bilateral DLPFC, IPL (inferior parietal lobule), and the left frontopolar area (FPA) (8). Importantly, further brain network investigations showed that enhanced FC was detected between the rostrolateral prefrontal (RLPFC), IPL, and DLPFC when participants were engaging in more complex reasoning (11). In particular, it was discovered that enhanced FC of lateral frontoparietal networks showed the relationship with better performance in relationship reasoning (11-13). However, these FC studies regarding the reasoning were mainly focused on visuo-spatial reasoning (14,15), analogical reasoning (16), and deductive reasoning (17) rather than the numerical inductive reasoning.
Interestingly, besides the problem representation and numerical inductive reasoning, planning also plays an essential role in the cognitive processing of arithmetic problem-solving. Planning refers to designing and evaluating a series of future actions to reach a desirable goal (18,19). Recent neuroimaging findings have stressed the interest of studying the brain activation and networks associated with planning. The neuroimaging results showed that the PFC exhibited significant relationship with planning during the Tower of London task (18,20), in which participants were required to plan a series of movements for moving a stack of discs and then execute the movements (21-23). In addition, during the Tower of London task, enhanced FC between the frontal and parietal regions was identified, which was more correlated with the planning phase rather than the execution phase (24). A recent study on autism based on the Tower of London task also showed that the frontal-parietal FC was correlated with the size of the anterior region of corpus callosum, which implied an anatomical basis underlying planning (25). Further neuroimaging work on planning exhibited that the anterior PFC involves evaluation and monitoring of the information while the posterior PFC involves maintenance and manipulation (26).
Since the calculation, planning, and reasoning involved the different cognitive processes during the arithmetical problem-solving, it is rational to hypothesize in this study that they might exhibit significant differences in brain activation and FC. In addition, previous neuroimaging studies illustrated that anterior PFC involves evaluation and monitoring of the information, which is more critical in planning than in calculation or numerical reasoning (26). As a result, it is also assumed in this study that enhanced effective connectivity (24) might be detected between the anterior prefrontal and posterior parietal cortex during planning compared to those during calculation and numerical reasoning.
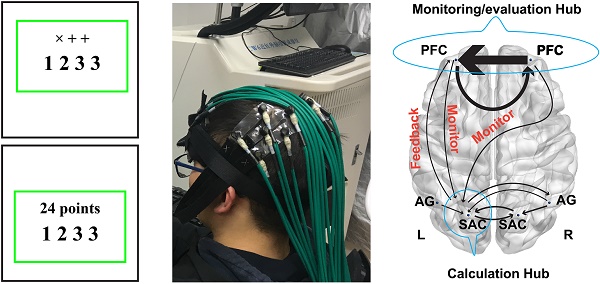
To date, there is no available paradigm to examine the brain activation and connectivity during planning in arithmetic problem-solving. To address this issue, an innovative task based on Chinese arithmetic problem-solving card game (24 points game: https://en.wikipedia.org/wiki/24_Game) was proposed for the present study, in which the players need to make full use of four randomly given cards and elementary arithmetic operations (the addition, subtraction, multiplication, and division) to generate the number 24. For example, when the participants are presented with the numbers 1, 2, 3, and 3, they need to decompose the goal as several sub-goals such as 4 and 6 (4 × 6 = 24), and then complete each sub-goal (1 + 3 = 4, 2 ×3 = 6) to achieve the final goal (4 × 6 = 24). The innovative paradigm consists of two conditions including the 24 points game and calculation conditions, in which the calculation condition serves as the control condition. With the minimum semantic demands as compared to that from word problem-solving, the 24 points game is a promising tool for the investigation of planning associated with arithmetic problem-solving. In addition, the number completion task was also adopted for the present work, which was able to inspect the numerical inductive reasoning to show the difference in brain activation and effective connectivity between planning and reasoning.
More importantly, during the 24 points game task, participants needed to report the answer orally, which might cause head movements and muscle tension. Consequently, the traditional neuroimaging methods such as functional magnetic resonance imaging (fMRI) and electroencephalograph (EEG) might not be the best choices for the present study due to fMRI's low tolerance to head movements (27) and EEG's sensitivity to muscle tension (28). In this study, functional near-infrared spectroscopy (fNIRS) was utilized to explore the brain activation and networks associated with arithmetic problem-solving due to its unbeatable advantages such as high tolerance of head motion and muscle tension, high flexibility and economic efficiency, and high temporal resolution (29-32). More specifically, besides the proposed 24 points game paradigm, a new scheme that combines Granger causality analysis (GCA) and fNIRS recordings is presented to test the hypothesis. The new scheme is able to identify the direct causal influences in local brain networks between various regions of interest (ROIs), which can inspect the difference in effective connectivity between the calculation, planning and reasoning. It is expected that this pilot work will pave a new avenue for an improved understanding of the neural underpinnings underlying arithmetic problem-solving.
Methods and Materials
Participants
Twenty-nine college students (15 females and 14 males; Mean age =21.1 years; age range= 18.2 - 25.4) were recruited from the University of Macau campus. All participants were right-handed with normal or corrected-to-normal vision and none of them had reported histories of neurological or psychiatric disorders. Written informed consent was collected from all participants prior to the experimental tests. The protocol for the present study was approved by the Ethics Committees of the University of Macau.
Procedures and Materials
The experimental tests were conducted in a quiet room, in which participants were instructed to perform two tasks in order: the numerical reasoning (number completion) task and the 24 points game task. The 24 points game task contained two conditions including the 24-points game condition and the calculation condition (control condition) and each condition had 20 trials. In addition, the numerical reasoning task also consisted of two conditions: the complex reasoning condition and the simple reasoning condition (control condition), in which each condition contained 20 trials as well. Each trial started with a thinking period with the stimulus displayed in the center of the screen, followed by the response period during which the stimulus was framed by a green rectangle and the rest period with a fixation cross displayed in the center of the monitor. It is noted that the duration of each period (Fig. 1) was different for various conditions of each task because of the differences in task difficulties and associated response time.
Schematic of the paradigm. (a) 24 points game; (b) Numerical reasoning; (c) Possible cognitive processes during the 24 points game task.
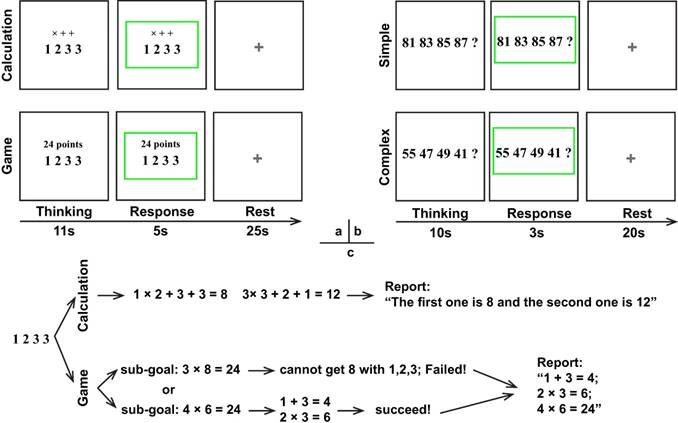
For the 24 points game task, four numbers ranged from 1-9 were displayed in the center of the monitor screen, and then participants needed to respond as soon as possible according to the instruction above the number series. Regarding the calculation condition, the instructions "× + +" were displayed above the numbers (Fig. 1) and participants were required to finish the calculation in order and reverse order. For example, regarding number series "1 2 3 3", participants should first finish the operation 1×2+3+3=8 and 3×3+2+1=12, and then reported “The first one is 8 and the second one is 12”. To minimize their memory load during the thinking period for the calculation condition, participants were allowed to write down the answer in a piece of paper but were not permitted to write down the operation process. By contrast, for the 24-points game condition, the instruction "24 points" was shown over the top of the numbers, which required participants to get 24 by using the combined operations of addition, subtracttion, multiplication, or division for the four numbers. During the response period, participants needed to report the operation process on how to achieve 24 or report "I don't know" if they really did not know the answer, whereas for the calculation condition they only needed to report the two answers in order. Unlike the calculation condition, no explicit solution was provided for the 24-points game condition. Consequently, participants had to design and evaluate a series of future actions, which was denoted as the planning process.
With regard to the numerical reasoning task, participants needed to discern the rules for the given series associated with four numbers and then quantify the fifth number and reported it during the response period. The simple reasoning condition involved concessive additions or subtractions. For example, the rule and answer for "81 83 85 87?" in the simple condition was respectively “rule: +2, +2, +2 + 2; answer: 89”. However, this is not the case for the complex reasoning condition, which involved two numeric rules. For example, the rules and answer for "70 66 61 57?" in the complex condition were respectively “rules: -4, -5, -4 - 5; answer: 52”.
fNIRS Data Acquisition and Preprocessing
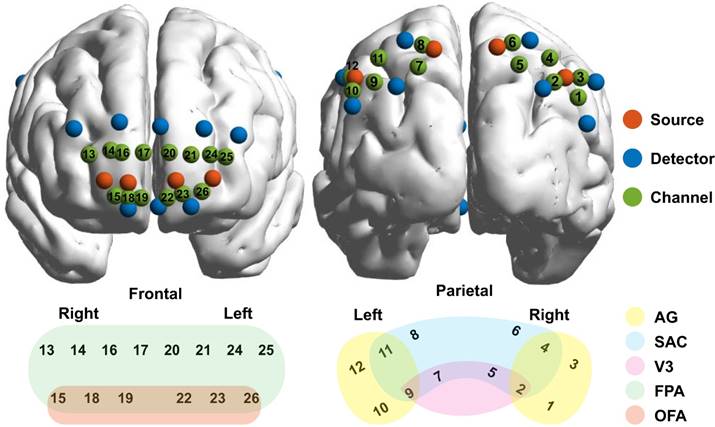
A CW6 fNIRS system (TechEn Inc., Milford, MA) was used to collect fNIRS data with sampling rate of 50 Hz. A home-made plastic patch was placed on the head to hold 8 sources and 16 detectors together with a fixed inter-optode distance of 3 cm. After data acquisition, a three-dimensional (3D) digitizer (PATRIOT, Polhemus, Colchester, Vermont, USA) was used to measure the 3D coordinates of all optodes for each participant. And then the coordinates were processed by using NIRS-SPM (33) to access the MNI coordinates and associated anatomical labels for all optodes as well as the generated 26 channels (see Table S1 in appendix). The optodes and 26 channels were further visualized on two brain templates according to their mean MNI coordinates by using BrainNet Viewer toolbox (http://www.nitrc.org/ projects/bnv/) (34), whereas the anatomical labels were also marked in various colors and displayed in Fig. 2.
The fNIRS signals were preprocessed with Homer2 software (35). As demonstrated in previous studies (36-38), the raw data were first converted to the optical density changes. After removing motion artifacts (39), the optical density signals were filtered with a low-pass filter of 0.2 Hz and were then converted to the HbO and HbR concentration changes. The concentration changes were normalized by subtracting the mean channel-wise concentration and then divided by the standard deviation (z-scores). Subsequently, data segmentation was also performed, in which the duration for each block consisted of a pre-stimulus period of 2 s, a stimulus period of 16 s for 24 points game task or 13 s for numerical reasoning task, and a post-stimuli period of 23 s for 24 points game task or 18 s for numerical reasoning task. Finally, the least squares model fitting procedure according to the signals in the first and last 2 s of each trial was performed for baseline correction to remove the possible physiological drifts (40,41).
Brain Activation
After the preprocessing was completed, the trial-averaged z-scores were extracted to indicate the brain activation for all channels for each participant. And then the grand-averaged z-scores for each condition of each task were also generated across all participants. In this study, only HbO signal was analyzed due to its superior contrast-to-noise ratio (42).
Multivariate Granger Causality Analysis
The Granger causality analysis (GCA) was used to map effective connectivity, in which the directional information provided by Granger causality (GC) offers the potential for defining the anatomical pathways that underlie neural interactions (43,44). Moreover, previous studies have proved that the GCA is sufficient to characterize the information flow of fNIRS signals (45-50).
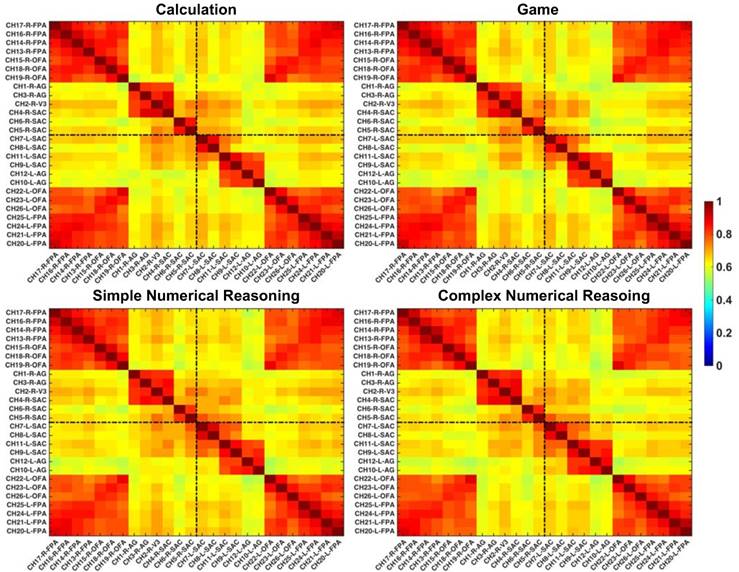
In this study, regions of interest (ROIs) were first identified with the functional connectivity analysis method, which were later utilized to reconstruct GC-based effective networks. Before the functional and effective connectivity analysis, the HbO signals were down-sampled to 2 Hz to ensure a reasonable model order for auto¬regressive modelling (51), and then the Pearson correlation coefficients between pairs of channels were calculated for each partici¬pant. After the Fisher's r-to-z transforma¬tion for the correlation coefficients (52), the z-values were averaged across participants and were subsequently transformed back to the r-values. The reformulated FC matrix was displayed in Fig. 3, in which six clusters were clearly identified in the cortex: the left and right FPA (channels 20~26 and channels 13~19), the left and right AG (channels 9~12 and channels 1~4), and the left and right SAC (channels 7,8 and channels 5,6). More interestingly, the identified ROIs based on functional connectivity analysis were also in line with the configurations of channels in Fig. 2.
Configurations of the optodes and channels. The sources, detectors, and channels were visualized on brain templates in the first row and were colored in red, blue, and green, respectively. Meanwhile, the channels and their associated brain regions were visualized in the second row with different color indicating different brain regions. AG, angular gyrus, part of Wernicke's area; SAC, somatosensory association cortex; V3, visual area 3; FPA, frontopolar; OFA, orbitofrontal area.
Grand-averaged FC matrixes. The brighter color denotes higher FC and the channels are labeled in the format of “channel-hemisphere-anatomical label”.
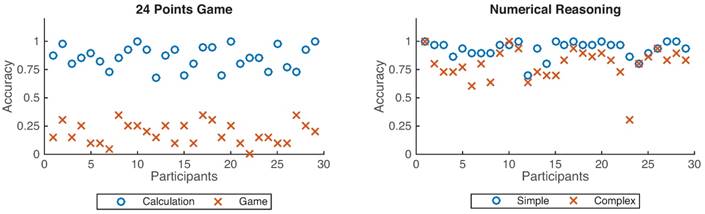
Accuracy distributions across 29 participants. The left figure denotes the accuracy for the 24 points game while the right one represents the numerical reasoning case. Blue circles denote the calculation and simple conditions, whereas the red cross define the game and complex conditions.
The HbO data from all channels within a ROI were averaged to indicate the brain activation of this ROI. The pre-stimulus (-2~0 s) baseline data from each ROI was excluded for further GCA. In addition, it is noted that in order to make time series data stationary, we removed the temporal mean from each trial and then divided the generated data by the temporal standard deviation. We also performed the same operation for ensemble mean and ensemble standard deviation (53,54).
Conditional GCA is carried out using the multivariate Granger causality toolbox (MVGC), which exhibits superior computational accuracy and statistical power (51,55). For conditional GCA, assuming that X and Y are time series from two ROIs, and Z is the data with the same length from the other ROIs that also imposes causality impacts on both X and Y. And then the temporal dynamics of two time series can be described by a bivariate autoregressive model:
(1)
(2)
In which t denotes the current time point, and k denotes the maximum number of lagged observations included in the model (model order, k<t), which is determined by Bayesian information criterion (56). The residuals ext and eyt denotes the prediction error of these two models, respectively.
Importantly, GC is easy to generalize to the multivariate (conditional) case in which the GC of Y on X is tested in the context of the other variables (Z). In this case, Y GC-causes X if knowing Y reduces the variance in X's prediction error when the effect from all other variables Z is also included in the regression model. It is vice versa for the case that X GC-causes Y:
(3)
(4)
As a result, the GC is determined by the comparison between variances of the prediction error in equations 2 (eyt) and 3 (exyt) or equations 1 (ext) and 4 (eyxt). In particular, the mathematical definition of GC is the logarithm of the ration of error variances:
(5)
(6)
Statistical Analysis
The mean accuracy of responses was quantified for each condition of the two tasks. And then paired t-tests were performed to reveal both the performance and brain activation differences between the two conditions for each task. In addition, the relationship between behavior performance and brain activation was also inspected by calculating the Pearson correlations between the accuracy and brain activation for the 24 points game and complex numerical reasoning task, respectively.
As the GCA results satisfy an F distribution (55,57), the F-statistic with the null hypothesis of zero was used to determine the statistical significance of GC coefficients. In addition, GC coefficients were normalized so that the paired t-tests can be performed to reveal the GC difference between any two conditions associated with each task (58,59). Specifically, for each participant, the GC coefficients were normalized according to, Zgci = (GCi -mean({GCi}))/std({GCi}), in which GCi is the GC from one channel to another, whereas {GCi} is the collection of all GC coefficients. And the normalized GC coefficients were subjected to the paired t-tests.
Results
Behavioral Results
As shown in Fig. 4, participants achieved better performance under the calculation condition than that from the 24-points game case (p < 0.001), and also better performance for the simple reasoning condition than that from the complex reasoning case (p < 0.001).
Brain Activation and Its Relationship with the Behavioral Performance
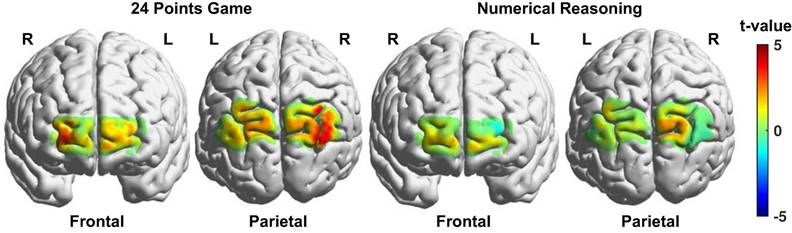
The brain activation differences between the game and calculation conditions for the 24 points game task and between the complex and simple reasoning conditions for the numerical reasoning task were respectively visualized in Fig. 5. And the channels that exhibited significant difference between the two conditions associated with each task were listed in Table 1. We discovered from Fig. 5 and Table 1 that multiple brain regions including the right visual area 3 (V3), angular gyrus (AG), bilateral somatosensory association cortex (SAC), frontopolar (FPA), and orbitofrontal area (OFA) exhibited enhanced activation for the game condition as compared to that from the calculation condition. By contrast, only three channels located in the right SAC and bilateral OFA showed higher activation for the complex reasoning condition as compared to that from the simple reasoning condition.
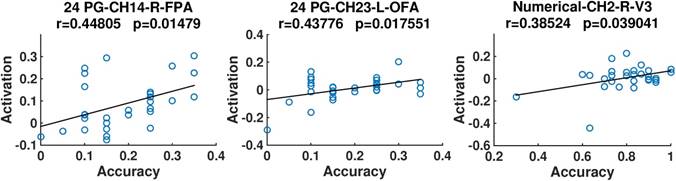
In addition, we discovered from Fig. 6 that for both the 24 points game and numerical reasoning tasks, the behavioral performance exhibited positive correlation with the brain activation. In particular, positive correlations were identified in the right FPA and left OFA for the 24 points game case, whereas for the numerical reasoning case, the positive relationship was revealed in the conjunction of SAC, V3, and AG (channel 2).
Brain activation difference maps between the two conditions (experimental - control) for the two tasks. The brighter color denotes higher t values resulted from the t-tests.
Paired t-test results for channels with significant activation.
| Contrasts | #ch | Label | p | t | df | SD | d | M1 | SE1 | M2 | SE2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| game - calculation | 2 | R-V3 | 0.001 | 3.77 | 28 | 0.188 | 0.785 | 0.120 | 0.025 | -0.012 | 0.036 |
| 3 | R-AG | 0.001 | 3.54 | 28 | 0.204 | 0.832 | 0.087 | 0.025 | -0.047 | 0.034 | |
| 4 | R-SAC | <0.001 | 4.50 | 28 | 0.189 | 1.018 | 0.140 | 0.023 | -0.018 | 0.034 | |
| 5 | R-SAC | 0.034 | 2.23 | 28 | 0.152 | 0.385 | 0.142 | 0.027 | 0.079 | 0.033 | |
| 7 | L-SAC | 0.033 | 2.25 | 28 | 0.199 | 0.472 | 0.066 | 0.026 | -0.018 | 0.038 | |
| 8 | L-SAC | 0.017 | 2.53 | 28 | 0.137 | 0.472 | 0.058 | 0.024 | -0.006 | 0.026 | |
| 11 | L-SAC | 0.043 | 2.12 | 28 | 0.187 | 0.463 | 0.089 | 0.029 | 0.015 | 0.031 | |
| 13 | R-FPA | 0.010 | 2.76 | 28 | 0.107 | 0.455 | 0.049 | 0.020 | -0.005 | 0.024 | |
| 14 | R-FPA | 0.005 | 3.08 | 28 | 0.096 | 0.464 | 0.084 | 0.021 | 0.029 | 0.023 | |
| 15 | R-OFA | 0.001 | 3.54 | 28 | 0.113 | 0.523 | 0.065 | 0.024 | -0.009 | 0.028 | |
| 19 | R-OFA | 0.018 | 2.51 | 28 | 0.067 | 0.301 | 0.018 | 0.018 | -0.013 | 0.020 | |
| 22 | L-OFA | 0.007 | 2.89 | 28 | 0.063 | 0.468 | 0.017 | 0.012 | -0.017 | 0.014 | |
| 23 | L-OFA | 0.035 | 2.21 | 28 | 0.100 | 0.368 | 0.008 | 0.017 | -0.033 | 0.024 | |
| 24 | L-FPA | 0.022 | 2.42 | 28 | 0.150 | 0.482 | 0.073 | 0.029 | 0.006 | 0.022 | |
| 26 | L-OFA | 0.016 | 2.57 | 28 | 0.100 | 0.473 | 0.061 | 0.018 | 0.014 | 0.019 | |
| Complex - Simple | 5 | R-SAC | 0.030 | 2.28 | 28 | 0.079 | 0.325 | 0.080 | 0.021 | 0.046 | 0.018 |
| 19 | R-OFA | 0.019 | 2.49 | 28 | 0.042 | 0.312 | 0.013 | 0.013 | -0.007 | 0.010 | |
| 22 | L-OFA | 0.039 | 2.16 | 28 | 0.046 | 0.301 | 0.008 | 0.013 | -0.010 | 0.009 |
Effective Connectivity
The averaged GC coefficients were visualized in matrix form in Fig. 7(a), whereas the effective connectivity was displayed on the brain templates in Fig. 7(b). In addition, detailed GCA results were listed in Table 2. Interestingly, we discovered from Fig. 7 that bidirectional connectome between the bilateral SAC and that between the bilateral prefrontal cortex (PFC), and effective connectivity from the right AG to bilateral SAC and that from the left AG to left SAC were clearly identified for various cases.
Scatter plots of the accuracy and activation. The correlation coefficients (r) and their significance level (p) are provided. Titles are organized according to the format of “task-channel-hemisphere-anatomical label”.
Effective connectivity for the two conditions associated with two tasks. The darker colors within the matrixes in (a) and thicker curves in (b) denote higher GCs.
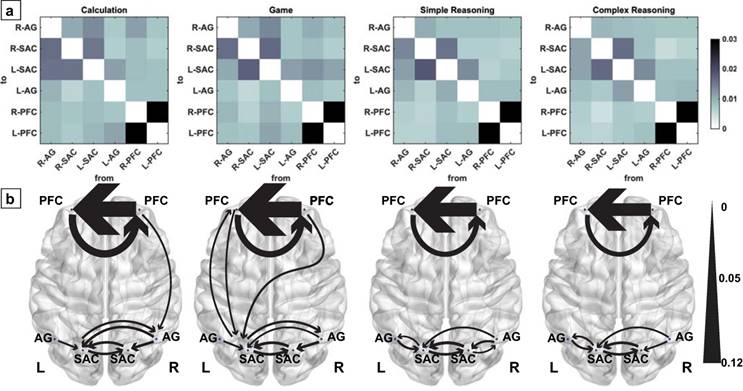
In particular, significant bidirectional connectome was observed between the left PFC and left SAC for the game condition associated with the 24 points game task although this is not the case for the calculation condition and the other two conditions associated with numerical reasoning task. Meanwhile, the effective connectivity was also confirmed from the right PFC to right AG for the calculation condition and that from the right PFC to left SAC for the game condition. By contrast, no effective connectivity between the prefrontal and parietal cortex was identified for the numerical reasoning task. In addition, the connection from the right SAC to right AG only was only identified in the simple reasoning condition of numerical reasoning task.
More importantly, all normalized GC coefficients were subjected to the paired t-tests to quantify the GC differences between the two conditions for each task. The generated t-values were visualized in matrix form in Fig. 8. We discovered that the game condition exhibited significant difference in the effective connectivity with the calculation condition for the 24 points game task. Specifically, compared to those from the calculation condition, decreased GCs were observed from the right AG to left SAC (t(28) = -2.20, p = 0.037, Cohen's d = -0.53) and from the left AG to left PFC (t(28) = -2.87, p = 0.008, Cohen's d = -0.56), while enhanced GCs were observed from the left SAC to left PFC (t(28) = 2.10, p = 0.045, Cohen's d = 0.48) as well as from the left (t(28) = 2.07, p = 0.048, Cohen's d = 0.40) and the right PFC (t(28) = 2.52, p = 0.018, Cohen's d = 0.50) to left SAC for the game condition.
By contrast, compared to the simple condition of numerical reasoning task, the complex condition showed significantly decreased effective connectivity from the right PFC to right SAC (t(28) = -2.14, p = 0.0416, Cohen's d = -0.52) and significantly increased effective connectivity from the left AG to right SAC (t(28) = 2.32, p = 0.028, Cohen's d = 0.37).
Significant GC coefficients for the four cases.
| Conditions | Source | Target | GC | p-value | p(FDR) |
|---|---|---|---|---|---|
| Calculation | R-AG | R-SAC | 0.016 | 0.0007 | 0.0064 |
| R-AG | L-SAS | 0.016 | 0.0011 | 0.0064 | |
| R-SAC | L-SAS | 0.016 | 0.0009 | 0.0064 | |
| L-SAS | R-AG | 0.014 | 0.0036 | 0.0154 | |
| L-SAS | R-SAC | 0.015 | 0.0014 | 0.0069 | |
| L-AG | L-SAS | 0.011 | 0.0119 | 0.0445 | |
| R-PFC | R-AG | 0.011 | 0.0134 | 0.0445 | |
| R-PFC | L-PFC | 0.101 | <0.0001 | <0.0001 | |
| L-PFC | R-PFC | 0.048 | <0.0001 | <0.0001 | |
| Game | R-AG | R-SAC | 0.016 | 0.0008 | 0.0045 |
| R-AG | L-SAS | 0.011 | 0.0177 | 0.0483 | |
| R-SAC | L-SAS | 0.017 | 0.0004 | 0.0036 | |
| L-SAS | R-AG | 0.014 | 0.0027 | 0.0137 | |
| L-SAS | R-SAC | 0.017 | 0.0005 | 0.0040 | |
| L-SAS | L-PFC | 0.011 | 0.0142 | 0.0451 | |
| L-AG | L-SAS | 0.012 | 0.0115 | 0.0433 | |
| R-PFC | L-SAS | 0.013 | 0.0048 | 0.0206 | |
| R-PFC | L-PFC | 0.103 | <0.0001 | <0.0001 | |
| L-PFC | L-SAS | 0.011 | 0.0150 | 0.0451 | |
| L-PFC | R-PFC | 0.040 | <0.0001 | <0.0001 | |
| Simple Reasoning | R-AG | R-SAC | 0.014 | 0.0008 | 0.0047 |
| R-AG | L-SAS | 0.011 | 0.0043 | 0.0184 | |
| R-SAC | R-AG | 0.010 | 0.0107 | 0.0358 | |
| R-SAC | L-SAS | 0.019 | <0.0001 | 0.0002 | |
| L-SAS | R-SAC | 0.016 | 0.0002 | 0.0014 | |
| L-SAS | L-AG | 0.010 | 0.0088 | 0.0328 | |
| L-AG | L-SAS | 0.013 | 0.0009 | 0.0047 | |
| R-PFC | L-PFC | 0.090 | <0.0001 | <0.0001 | |
| L-PFC | R-PFC | 0.034 | <0.0001 | <0.0001 | |
| Complex Reasoning | R-AG | R-SAC | 0.011 | 0.0051 | 0.0197 |
| R-AG | L-SAS | 0.011 | 0.0052 | 0.0197 | |
| R-SAC | L-SAS | 0.017 | 0.0001 | 0.0010 | |
| L-SAS | R-SAC | 0.016 | 0.0002 | 0.0012 | |
| L-SAS | L-AG | 0.011 | 0.0040 | 0.0197 | |
| L-AG | L-SAS | 0.013 | 0.0010 | 0.0061 | |
| R-PFC | L-PFC | 0.082 | <0.0001 | <0.0001 | |
| L-PFC | R-PFC | 0.030 | <0.0001 | <0.0001 |
T value matrixes generated from paired t-tests. The colors denote the t values and the significant differences in effective connectivity are highlighted in white squares.
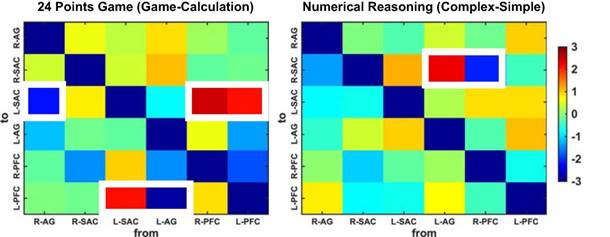
Further, a bootstrap method (60) was adopted to quantify the temporal relations across lags. In brief, the time series in each trial were randomly but synchronously shuffled for 1000 times and were subjected to GCA. Such procedure interrupted the temporal relations across lags. Thus, the larger portion of the iterations, which were lower than the GC calculated from the original data, denoted the stronger directional influences beyond the temporal correlations. Subsequently, paired t-tests were performed on the portions for each GC. With this procedure, we discovered that the game condition in 24 points game task exhibited decreased connectivity from the left AG to left PFC (t(28) = -2.72, p = 0.01, Cohen's d = -0.69) as compared to the calculation case. By contrast, compared to the simple case, the complex case of numerical reasoning task exhibited increased connectivity from the right FA to left SAC (t(28) = 2.44, p = 0.02, Cohen's d = 0.60).
Discussion
Our results supported the primary hypothesis that planning, calculation and reasoning exhibited significant difference in the effective brain connectivity. In particular, the effective connectivity between the anterior frontal and posterior parietal cortex was more closely related to planning rather than reasoning.
We discovered that compared to the calculation condition, the 24 points game case showed enhanced and right lateralized brain activation across broad areas in the frontal and parietal cortex, as illustrated in the activation maps in Fig. 5. Interestingly, a recent meta-analysis revealed that the IPL and premotor cortex were right lateralized during planning (18). Meanwhile, a recent review work also demonstrated the rostrolateral PFC can served as a superordinate region during the hierarchical control of behavior (61). Our neuroimaging results indicated that the 24 points game was mainly involved in planning processing rather than the calculation, and the cognitive component of planning shares the same neural substrate as other goal-directed behaviors. In addition, compared to the simple reasoning condition, the complex reasoning case also elicited activation in the right SAC and bilateral OFA. The activation pattern was consistent with previous studies (10).
In addition, previous correlation analysis showed that the planning performance was regulated by the activation in right FPA and left OFA, which is critical for the monitoring of information (26). However, the reasoning performance was regulated by the activation in the conjunction of SAC, V3, and AG, which are critical for the representation of number quantities (3). Thus, our findings implied that the performance of planning is mainly regulated by the monitoring process, whereas the performance of numerical inductive reasoning is basically regulated by the calculation demands.
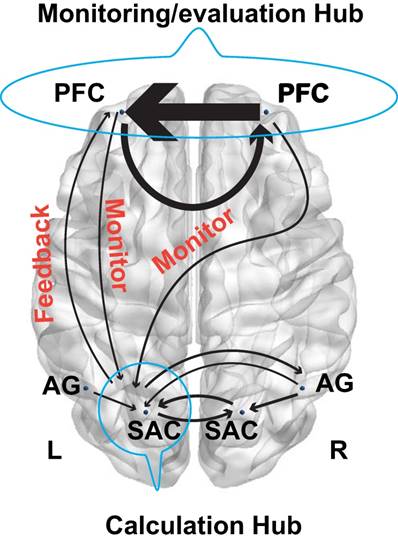
More importantly, the GCA results demonstrated that the left SAC was a crucial hub for the fronto-parietal network. In particular, its interaction with other brain regions such as the bilateral AG and right SAC provided a common effective network supporting the number processing during the arithmetic problem-solving. However, the interactions among the fronto-parietal network can effectively characterize the cognitive processing of calculation, planning, and reasoning. Specifically, the effective connectivity between the frontal and parietal cortex exhibited significant difference between the calculation, planning, and reasoning. For example, regarding the calculation, the right PFC had direct influence on the right AG, whereas the right AG also influenced the neural activities in bilateral SAC. These new findings were in line with a recent study, which discovered that lesions in the right AG impaired the mental calculation (62). Our results also implied that the polynomial operations are modulated by the right PFC. Interestingly, a reciprocal connectivity between the frontal and parietal cortex was identified for the 24 points game condition but not in the calculation conditions or reasoning task. As a result, the bilateral PFC directly affected the neural activities in the left SAC, and concurrently the left SAC also imposed influence on the left PFC. More interestingly, the brain networks in Fig. 7 might imply a monitoring- feedback-evaluation process during planning in the arithmetic problem-solving, in which the PFC serves as the monitoring and evaluation hub while the left SAC serves as the calculation hub, as illustrated in Fig. 9. For example, when the numbers “1 2 3 3” are combined together to generate number 24, the sub-goals 4 and 6 (4 × 6 = 24) might easily be achieved by (1+3)×(2×3) (monitor the mental calculation to achieve the sub-goal, and then evaluate the correct feedback). Likewise, we might also construct the sub-goals as 3 and 8 (3 × 8 = 24). However, we cannot achieve 8 with the left numbers 1 2 3 (incorrect feedback). Consequently, we have to adjust our sub- goals in the second step and perform the monitoring- feedback-evaluation again. Such problem- solving framework is worth further investigation in the future.
The t-tests and bootstrap results can also be interpreted according to this framework. Enhanced reciprocal connectivity between the frontal and parietal cortex was identified in the 24 points game condition as compared to the calculation condition. By contrast, enhanced connectivity from the right AG to left SAC and that from the left AG to left PFC were identified in the calculation condition as compared to the game condition. The increased connectivity from the left AG to left PFC was also revealed by the bootstrap method. Our findings confirmed that the cognitive process in 24 points game was monitored or planned by the frontal cortex although this is not the case for the calculation condition.
Unlike the 24 points game task, the F-test showed that the frontal and parietal cortex exhibited no effective connectivity for both conditions of numerical reasoning task. However, the bootstrap results demonstrated that the monitoring process from the right PFC to left SAC was still predominant in complex numerical inductive reasoning rather than the simple one. The t-tests results showed that compared to the simple reasoning, the complex reasoning exhibited decreased connectivity from the right PFC to right SAC, and increased connectivity from the left AG to right SAC. Our findings also indicated that the numerical inductive reasoning, although still needed to the monitoring from the frontal cortex as other reasoning process did, can process the information in a more independent way as compare to the planning process.
Model schematic showed monitoring and feedback processing.
Further, the present study not only proposed a novel paradigm that can effectively examine the planning during arithmetic problem-solving, but also has important practical implications for the evaluation of efficacy of mathematics education. The 24 points game has been playing in China since the 1960s, which is now widely used in math classes in China. Meanwhile, it also has been introduced to North American at least for 30 years (https://www.24 game.com/t-about-24gameanniversary.aspx.). However, the cognitive components in playing this game and their neural substrates remain unknown. This study revealed that the 24 points game, as compared to the widely used arithmetic exercises like the calculation and number series completion, elicited more engagement and interactions in the fronto-parietal network. Hence it provides an index for the evaluation of efficacy of mathematics education using arithmetic games, which might contribute to the emerging field of neuroeducation (63).
Limitations and Conclusions
There were several potential limitations to this study. Firstly, only part of brain cortex was covered by the patch due to the limited optodes. In addition, the order of the 24 points and numerical reasoning tasks was not counterbalanced, whose effect should be further investigated in the future.
In conclusion, the present study examined the differences in brain activation and effective connectivity between the calculation, planning, and reasoning. We discovered that compared to the calculation, planning showed enhanced and right lateralized brain activation across broad areas in the frontal and parietal cortex. By contrast, compared to the simple reasoning, only a small part of the frontal and parietal cortex exhibited high activation for the complexity reasoning. Further, the performance of planning showed the correlation with the activation in frontal cortex, whereas the performance of reasoning was correlated with the activation in the parietal cortex. More importantly, by combining the emerging technologies (fNIRS and GCA) with a novel paradigm (24 points game), we discovered that the directional effective connectivity between the anterior frontal and posterior parietal cortex was more closely related to planning rather than reasoning. Our study proved that the fNIRS is a sufficient technique to characterize the effective connectivity for the construction of directional networks, which provides evidence in favor of future analog fNIRS studies.
Supplementary Material
Supplementary table S1.
Acknowledgements
This study was supported by MYRG2016-00110-FHS and MYRG 2018-00081-FHS grants from the University of Macau, and FDCT 0011/2018/A1 and FDCT 025/2015/A1 grants from Macau government.
Competing Interests
The authors have declared that no competing interest exists.
References
1. Fuchs LS, Fuchs D, Stuebing K. et al. Problem solving and computational skill: Are they shared or distinct aspects of mathematical cognition? J Educ Psychol. 2008;100:30-47
2. Duncker K. On problem-solving. Psychol Monogr. 1945;58:1
3. Dehaene S, Piazza M, Pinel P. et al. Three parietal circuits for number processing. Cogn Neuropsychol. 2003;20:487-506
4. Zhou X, Li M, Li L. et al. The semantic system is involved in mathematical problem solving. Neuroimage. 2018;166:360-370
5. Evans TM, Kochalka J, Ngoon TJ. et al. Brain Structural Integrity and Intrinsic Functional Connectivity Forecast 6 Year Longitudinal Growth in Children's Numerical Abilities. J Neurosci. 2015;35:11743-11750
6. Zhao H, Li X, Karolis V. et al. Arithmetic learning modifies the functional connectivity of the fronto-parietal network. Cortex. 2018:1-12
7. Fuchs LS, Geary DC, Fuchs D. et al. Sources of Individual Differences in Emerging Competence With Numeration Understanding Versus Multidigit Calculation Skill. J Educ Psychol. 2014;106:482-498
8. Xiao F, Li P, Long C-Q. et al. Relational complexity modulates activity in the prefrontal cortex during numerical inductive reasoning: An fMRI study. Biol Psychol. 2014;101:61-68
9. Devlin JT, Matthews PM, Rushworth MFS. Semantic processing in the left inferior prefrontal cortex: A combined functional magnetic resonance imaging and transcranial magnetic stimulation study. J Cogn Neurosci. 2003;15:71-84
10. Liang P, Jia X, Taatgen NA. et al. Activity in the fronto-parietal network indicates numerical inductive reasoning beyond calculation: An fMRI study combined with a cognitive model. Sci Rep. 2016;6:1-10
11. Vendetti MS, Bunge SA. Evolutionary and developmental changes in the lateral frontoparietal network: A little goes a long way for higher-level cognition. Neuron. 2014;84:906-917
12. Langeslag SJE, Schmidt M, Ghassabian A. et al. Functional connectivity between parietal and frontal brain regions and intelligence in young children: The Generation R study. Hum Brain Mapp. 2013;34:3299-3307
13. Wendelken C, Ferrer E, Ghetti S. et al. Frontoparietal Structural Connectivity in Childhood Predicts Development of Functional Connectivity and Reasoning Ability: A Large-Scale Longitudinal Investigation. J Neurosci. 2017;37:8549-8558
14. Ebisch SJH, Mantini D, Romanelli R. et al. Long-range functional interactions of anterior insula and medial frontal cortex are differently modulated by visuospatial and inductive reasoning tasks. Neuroimage. 2013;78:426-438
15. Bazargani N, Hillebrandt H, Christoff K. et al. Developmental changes in effective connectivity associated with relational reasoning. Hum Brain Mapp. 2014;35:3262-3276
16. Krawczyk DC. The cognition and neuroscience of relational reasoning. Brain Res. 2012;1428:13-23
17. Cocchi L, Halford GS, Zalesky A. et al. Complexity in relational processing predicts changes in functional brain network dynamics. Cereb Cortex. 2014;24:2283-2296
18. Nitschke K, Köstering L, Finkel L. et al. A Meta-analysis on the neural basis of planning: Activation likelihood estimation of functional brain imaging results in the Tower of London task. Hum Brain Mapp. 2017;38:396-413
19. van den Heuvel OA, Groenewegen HJ, Barkhof F. et al. Frontostriatal system in planning complexity: a parametric functional magnetic resonance version of tower of london task. Neuroimage. 2003;18:367-374
20. Koechlin E, Corrado G, Pietrini P. et al. Dissociating the role of the medial and lateral anterior prefrontal cortex in human planning. Proc Natl Acad Sci. 2000;97:7651-7656
21. Ward G, Oxford U. Planning and Problem-solving Using the Five-disc Tower of London Task. Q J Exp Psychol. 1997;50A:49-78
22. Shallice T. Specific impairments of planning. Philos Trans R Soc Lond B Biol Sci. Epub ahead of print. 1982 DOI: 10.1098/rstb.1982.0082
23. Fincham JM, Carter CS, van Veen V. et al. Neural mechanisms of planning: A computational analysis using event-related fMRI. Proc Natl Acad Sci. 2002;99:3346-3351
24. Alchihabi A, Kivilicim BB, Newman SD. et al. A dynamic network representation of fMRI for modeling and analyzing the problem solving task. Proc - Int Symp Biomed Imaging. 2018;5:114-117
25. Just MA, Cherkassky VL, Keller TA. et al. Functional and anatomical cortical underconnectivity in autism: Evidence from an fmri study of an executive function task and corpus callosum morphometry. Cereb Cortex. 2007;17:951-961
26. Wagner G, Koch K, Reichenbach JR. et al. The special involvement of the rostrolateral prefrontal cortex in planning abilities: An event-related fMRI study with the Tower of London paradigm. Neuropsychologia. 2006;44:2337-2347
27. Cui X, Baker JM, Liu N. et al. Sensitivity of fNIRS measurement to head motion: An applied use of smartphones in the lab. J Neurosci Methods. 2015;245:37-43
28. Izzetoglu K, Bunce S, Onaral B. et al. Functional optical brain imaging using near-infrared during cognitive tasks. Int J Hum Comput Interact. 2004;17:211-227
29. Yuan Z. Combining independent component analysis and Granger causality to investigate brain network dynamics with fNIRS measurements. Biomed Opt Express. 2013;4:2629
30. Yuan Z, Ye J. Fusion of fNIRS and fMRI data: identifying when and where hemodynamic signals are changing in human brains. Front Hum Neurosci. 2013;7:676
31. Yuan Z. Combining ICA and Granger causality: a novel tool for investigation of brain dynamics and brain oscillations using fNIRS measurements. In: Hirschberg H, Madsen SJ, Jansen ED, et al. (eds) Proceedings of SPIE, p. 89280I.
32. Ieong HF, Yuan Z. Emotion recognition and its relation to prefrontal function and network in heroin plus nicotine dependence: a pilot study. Neurophotonics. 2018;5:1
33. Ye JC, Tak S, Jang KE. et al. NIRS-SPM: Statistical parametric mapping for near-infrared spectroscopy. Neuroimage. 2009;44:428-447
34. Xia M, Wang J, He Y. BrainNet Viewer: A Network Visualization Tool for Human Brain Connectomics. PLoS One. 2013;8:e68910
35. Huppert TJ, Diamond SG, Franceschini MA. et al. HomER: a review of time-series analysis methods for near-infrared spectroscopy of the brain. Appl Opt. 2009;48:D280
36. Lu CM, Zhang YJ, Biswal BB. et al. Use of fNIRS to assess resting state functional connectivity. J Neurosci Methods. 2010;186:242-249
37. He Y, Wang M-Y, Li D. et al. Optical mapping of brain activation during the English to Chinese and Chinese to English sight translation. Biomed Opt Express. 2017;8:5399
38. Ding XP, Sai L, Fu G. et al. Neural correlates of second-order verbal deception: A functional near-infrared spectroscopy (fNIRS) study. Neuroimage. 2014;87:505-514
39. Scholkmann F, Spichtig S, Muehlemann T. et al. How to detect and reduce movement artifacts in near-infrared imaging using moving standard deviation and spline interpolation. Physiol Meas. 2010;31:649-662
40. Inamoto K, Sakuma S, Ariji Y. et al. Measurement of cerebral blood volume dynamics during volitional swallowing using functional near-infrared spectroscopy: An exploratory study. Neurosci Lett. 2015;588:67-71
41. Homae F, Watanabe H, Nakano T. et al. Prosodic processing in the developing brain. Neurosci Res. 2007;59:29-39
42. Strangman G, Culver JP, Thompson JH. et al. A quantitative comparison of simultaneous BOLD fMRI and NIRS recordings during functional brain activation. Neuroimage. 2002;17:719-731
43. Geweke JF. Measures of conditional linear dependence and feedback between time series. J Am Stat Assoc. 1984;79:907-915
44. Granger CWJ. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica. Epub ahead of print. 1969 DOI: 10.2307/1912791
45. Wan N, Hancock AS, Moon TK. et al. A functional near-infrared spectroscopic investigation of speech production during reading. Hum Brain Mapp. 2018;39:1428-1437
46. Zhou G, Liu J, Ding XP. et al. Development of Effective Connectivity during Own- and Other-Race Face Processing: A Granger Causality Analysis. Front Hum Neurosci. 2016;10:1-14
47. Liu Z, Zhang M, Xu G. et al. Effective Connectivity Analysis of the Brain Network in Drivers during Actual Driving Using Near-Infrared Spectroscopy. Front Behav Neurosci. 2017;11:1-11
48. Cao J, Wang X, Liu H. et al. Directional changes in information flow between human brain cortical regions after application of anodal transcranial direct current stimulation (tDCS) over Broca's area. Biomed Opt Express. 2018;9:5296
49. Hoppes CW, Sparto PJ, Whitney SL. et al. Functional near-infrared spectroscopy during optic flow with and without fixation. PLoS One. 2018;13:1-14
50. Vergotte G, Torre K, Chirumamilla VC. et al. Dynamics of the human brain network revealed by time-frequency effective connectivity in fNIRS. Biomed Opt Express. 2017;8:5326
51. Seth AK. A MATLAB toolbox for Granger causal connectivity analysis. J Neurosci Methods. 2010;186:262-273
52. Fisher RA. On the probable error of a coefficient of correlation an found from a small sample. Metron. 1921;1:3-32
53. Cui J, Xu L, Bressler SL. et al. BSMART: A Matlab/C toolbox for analysis of multichannel neural time series. Neural Networks. 2008;21:1094-1104
54. Ding M, Bressler SL, Yang W. et al. Short-window spectral analysis of cortical event-related potentials by adaptive multivariate autoregressive modeling: Data preprocessing, model validation, and variability assessment. Biol Cybern. 2000;83:35-45
55. Barnett L, Seth AK. The MVGC multivariate Granger causality toolbox: A new approach to Granger-causal inference. J Neurosci Methods. 2014;223:50-68
56. Schwarz G. Estimating the Dimension of a Model. Ann Stat. 1978;6:461-464
57. Bressler SL, Seth AK. Wiener-Granger Causality: A well established methodology. Neuroimage. 2011;58:323-329
58. Wen X, Yao L, Liu Y. et al. Causal Interactions in Attention Networks Predict Behavioral Performance. J Neurosci. 2012;32:1284-1292
59. Zang ZX, Yan CG, Dong ZY. et al. Granger causality analysis implementation on MATLAB: A graphic user interface toolkit for fMRI data processing. J Neurosci Methods. 2012;203:418-426
60. Bradleyel E, Tibshirani R. An introduction to the Bootstrap. CRC press. Epub ahead of print. 1993 DOI: 10.1016/j.yapd.2013.04.017
61. Badre D, Nee DE. Frontal Cortex and the Hierarchical Control of Behavior. Trends Cogn Sci. 2018;22:170-188
62. Benavides-Varela S, Piva D, Burgio F. et al. Re-assessing acalculia: Distinguishing spatial and purely arithmetical deficits in right-hemisphere damaged patients. Cortex. 2017;88:151-164
63. Ansari D, De Smedt B, Grabner RH. Neuroeducation - A critical overview of an emerging field. Neuroethics. 2012;5:105-117
Author contact
![]() Corresponding author: Prof. Zhen Yuan; Email: zhenyuanedu.mo
Corresponding author: Prof. Zhen Yuan; Email: zhenyuanedu.mo

 Global reach, higher impact
Global reach, higher impact